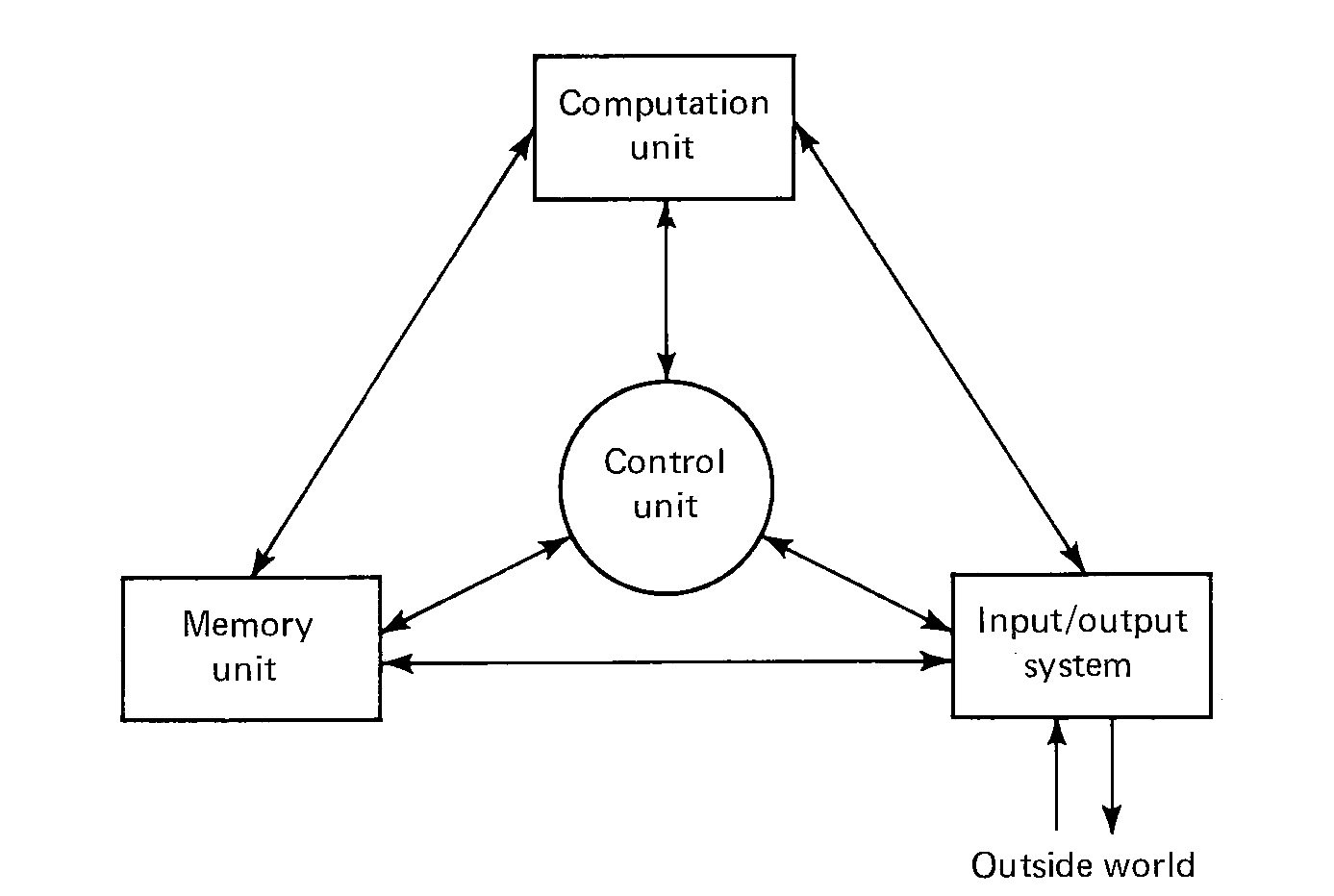
FIGURE 1.1 Basic components of a computer.
Computers, like automobiles, television, and telephones, are becoming more and more an integral part of our society. As such, more and more people come into regular contact with computers. Most of these people know how to use their computers only for specific purposes, although an increasing number of people know how to program them, and hence are able to solve new problems by using computers. Most of these people know how to program in a higher-level language, such as Basic, Fortran, Cobol, Algol, or PL/I. We assume that you know how to program in one of these languages.
However, although many people know how to use automobiles, televisions, telephones, and now computers, few people really understand how they work internally. Thus, there is a need for automotive engineers, electronics specialists, and assembly language programmers. There is a need for people who understand how a computer system works, and why it is designed the way that it is. In the case of computers, there are two major components to understand: the hardware (electronics), and the software (programs). It is the latter, the software, that we are mainly concerned with in this book. However, we also consider how the hardware operates, from a programmer's point of view, to make clear how it influences the software.
This chapter reviews the basic organization of computers, to provide a background for the software considerations of later chapters. You should be familiar with most of this material already, but this review will assure that we all agree on the basic information.
FIGURE 1.1 Basic components of a computer.
We can understand a computer by studying each of its components separately and by examining how they fit together to form a computing system. The four basic components of a computer are shown in Figure 1.1. These four elements are: (a) a memory unit, (b) a computation unit, (c) an input and output system, and (d) a control unit. The arrows between the different components in Figure 1.1 illustrate that information may travel freely between any two components of the computer. Some information paths may be missing in some computers. For example, in many systems there is no direct connection between the computation unit and the input/output system.
The memory unit functions as a storage device in the computer, storing data and programs for the computer. The computation unit does the actual computing of the computer -- the additions, subtractions, multiplications, divisions, comparisons, and so on. The input/output (I/O) system allows the computer to communicate with the outside world, to accept new data and programs and to deliver the results of the computer's work back to the outside world. The control unit uses the programs stored in the computer's memory to determine the proper sequence of operations to be performed by the computer. The control unit issues commands to the other components of the system directing the memory unit to pass information to and from the computation unit and the I/O system, telling the computation unit what operation to perform and where to put the results, and so forth.
Each of these components is discussed in more detail below. Every computer must have these four basic components, although the organization of a specific computer may structure and utilize them in its own manner. We are therefore presenting general organizational features of computers, at the moment. In Chapters 2, 3, and 10 we consider specific computers and their organization.
A very necessary capability for a computer is the ability to store, and retrieve, information. Memory size and speed are often the limiting factors in the operation of modern computers. For many of today's computing problems it is essential that the computer be able to quickly access large amounts of data stored in memory.
We consider the memory unit from two different points of view. We first consider the physical organization of a memory unit. This will give us a foundation from which we can investigate the logical organization of the memory unit.
For the past twenty years, the magnetic core has been the major form of computer memory. More recently, semiconductor memories have been developed to the point that most new computer memories are likely to be semiconductor memories rather than core memories. The major deciding factors between the two have been speed and cost. Semiconductor memories are undeniably faster, but until recently have also been more expensive.
Core memories have been used for many years and will undoubtedly continue to be used widely. They have been the main form of computer main memory for almost twenty years. Since semiconductor memories have been trying to replace core memories, they have been built to look very much like core memories, from a functional point of view. Therefore, we present some basic aspects of computer memories in terms of core memories first, and then we consider semiconductor memories.
Figure 1.2 is a drawing of a magnetic core. Cores are very small (from 0.02 to 0.05 inches in diameter) doughnut-shaped pieces of metallic ferrite materials which are mainly iron oxide. They have the useful property of being able to be easily magnetized in either of two directions: clockwise or counterclockwise. A core can be magnetized by passing an electrical current along the wire through the hole in the center of the core for a short time. Current in one direction (+) will magnetize the core in one direction (clockwise), and current in the opposite direction (-) will magnetize the core in the opposite direction (counterclockwise). Once the core has been magnetized in a given direction, it will remain magnetized in that direction for an indefinitely long time (unless it is deliberately remagnetized in the opposite direction, of course). This allows a core to store either of two states, which can be arbitrarily assigned the symbols 0 and 1 (or + and -, or A and B, etc.).
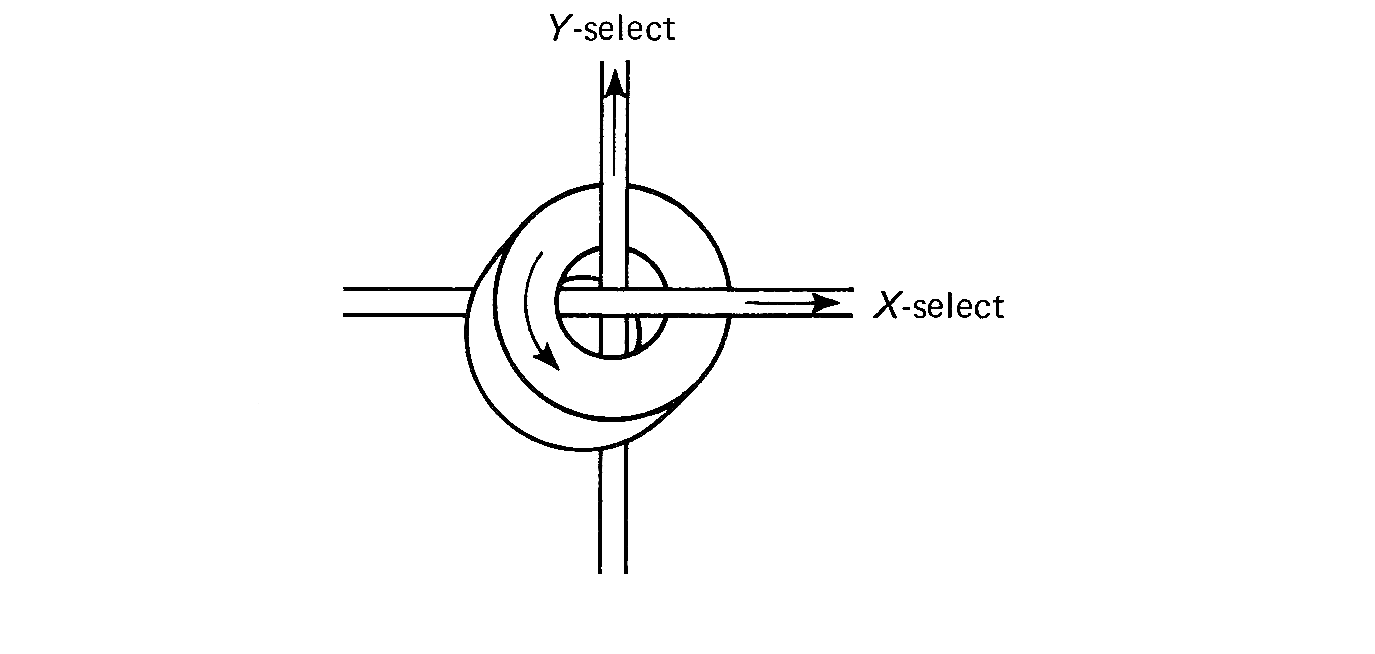FIGURE 1.2 A magnetic core (much enlarged)
The magnetic core was chosen as the basic storage unit because of several desirable physical properties. It can be easily and quickly switched from one state to the other by passing an electrical current through the core. A positive current will put the core in one state, while a negative current will put the core in the other state. The switching time of a core depends again upon the size and composition of the core, but is typically in the range 0.25 to 2.5 microseconds (10-6 seconds). The switching time is the time it takes the core to switch from one state to the other.
Individual cores are organized into larger units called core planes. A core plane is a two-dimensional rectangular array of cores. Figure 1.3 illustrates the basic design of a core plane. A specific core can be selected by choosing a specific X-select and Y-select wire. For example, in Figure 1.3 the core at the intersection of the X5 and the Y2 wires has been "selected."
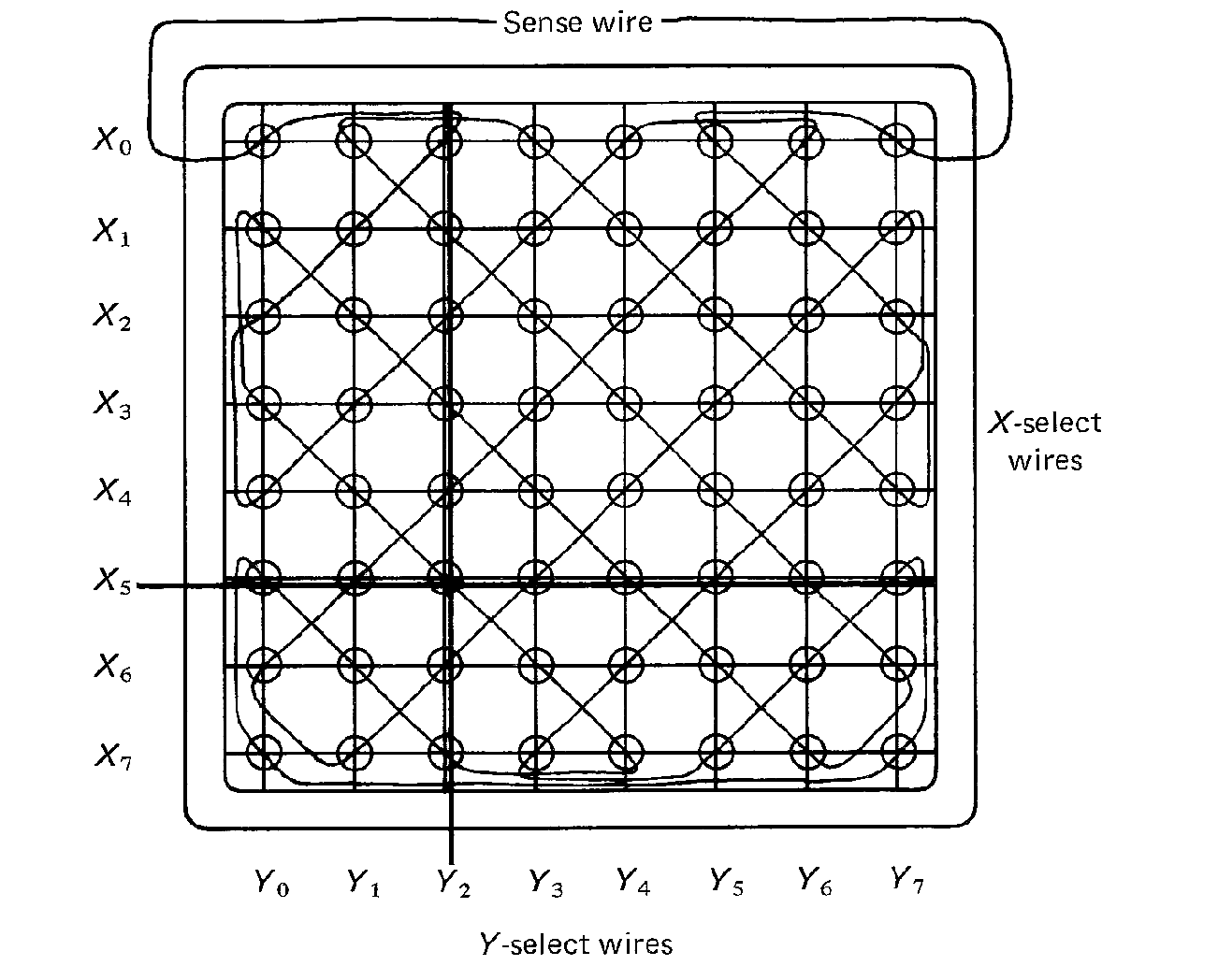FIGURE 1.3 Core plane showing X-select
and Y-select wires and sense wire.
Cores can be written by setting their magnetic state to one of the two possible states. They can be read by sensing their current state. Core memories have destructive readout; that is, reading a core can be accomplished only by disturbing the state of the core. It is necessary to rewrite the information back to the core to preserve it. This defines a read-write cycle for the memory. Whenever a core is read, it is immediately rewritten. For a write, the "old" information is read out, and the "new" information is written instead. The cycle time for a memory is at least twice its switching time, and typical core memory cycle times are 0.5 to 5 microseconds. Notice that the access time (time to read information) is generally only half the cycle time.
Core planes are "stacked," one on top of another, to form memory modules. All the cores selected by a specific pair of X and Y wires (one core from each core plane) are used to form a word of memory. To read or write a word from memory, one core from each core plane is read and written, simultaneously. The specific core in each core plane is selected by a memory address register which specifies the X-select and Y-select wires to be used. The result from a read is put into a memory data register. The contents of this register are then used to restore the selected word. In a write operation, the result of the read operation is not used to set the memory data register, but is simply discarded. The word in memory is then written from the memory data register.
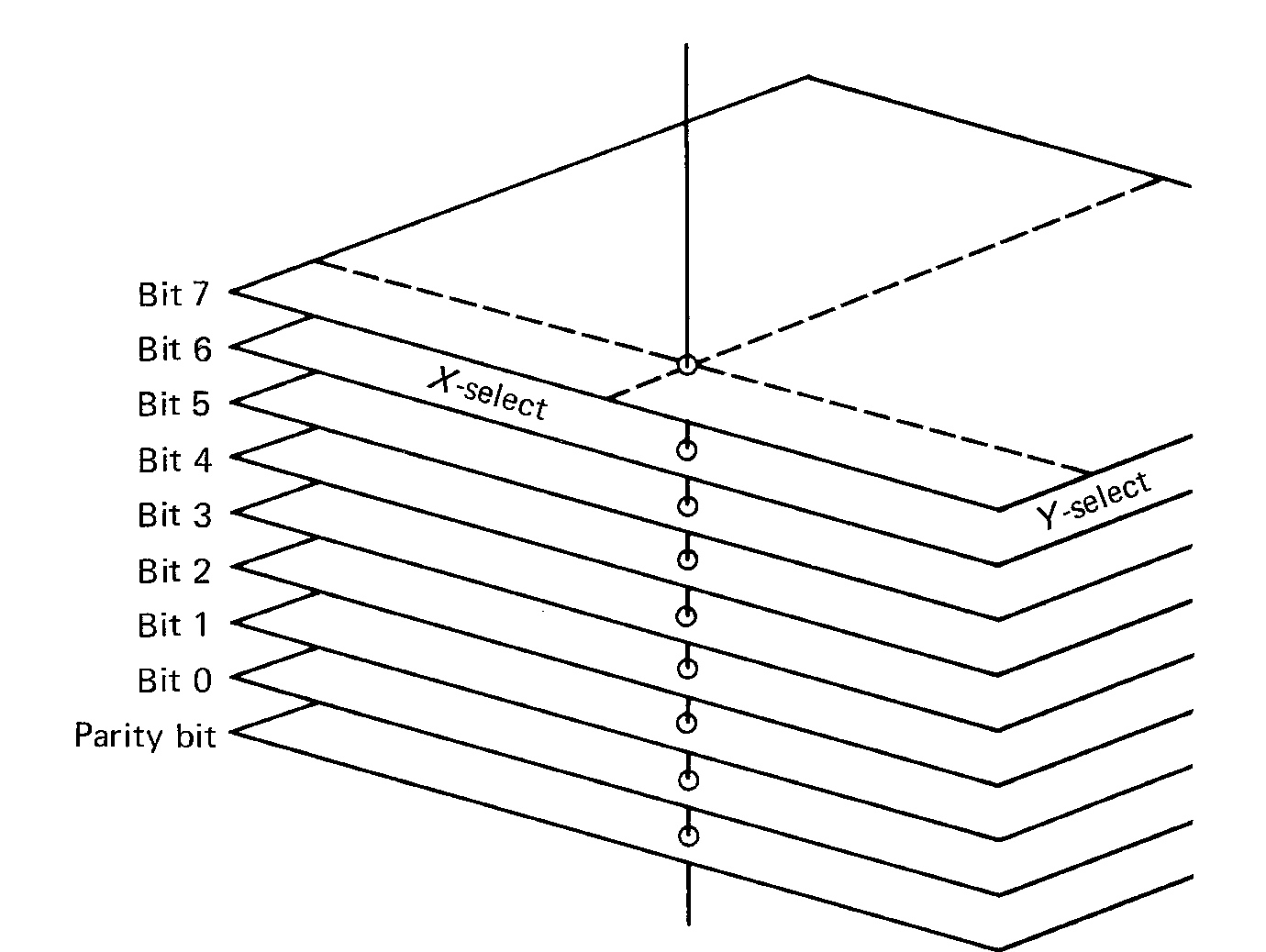FIGURE 1.4 Core planes stacked to form a memory module;
one bit from each core plane forms a word (or byte).
The memory address register and the memory data register, along with a single read or write line, are the interface of the memory module to the rest of the computer system (Figure 1.5). To read from memory, another component of the computer system puts the address of the desired word in the memory address register, puts "READ" on the read-write selector, and waits for the first half of the read-write cycle. After this first half, the contents of the addressed word are in the memory data register and may be used. They are also written back into memory to restore the cores of that word. For a write, the contents of the word to be written are put in the memory data register, and the read-write wire is set to "WRITE". After the entire read-write cycle is over, the addressed word will have its new contents.
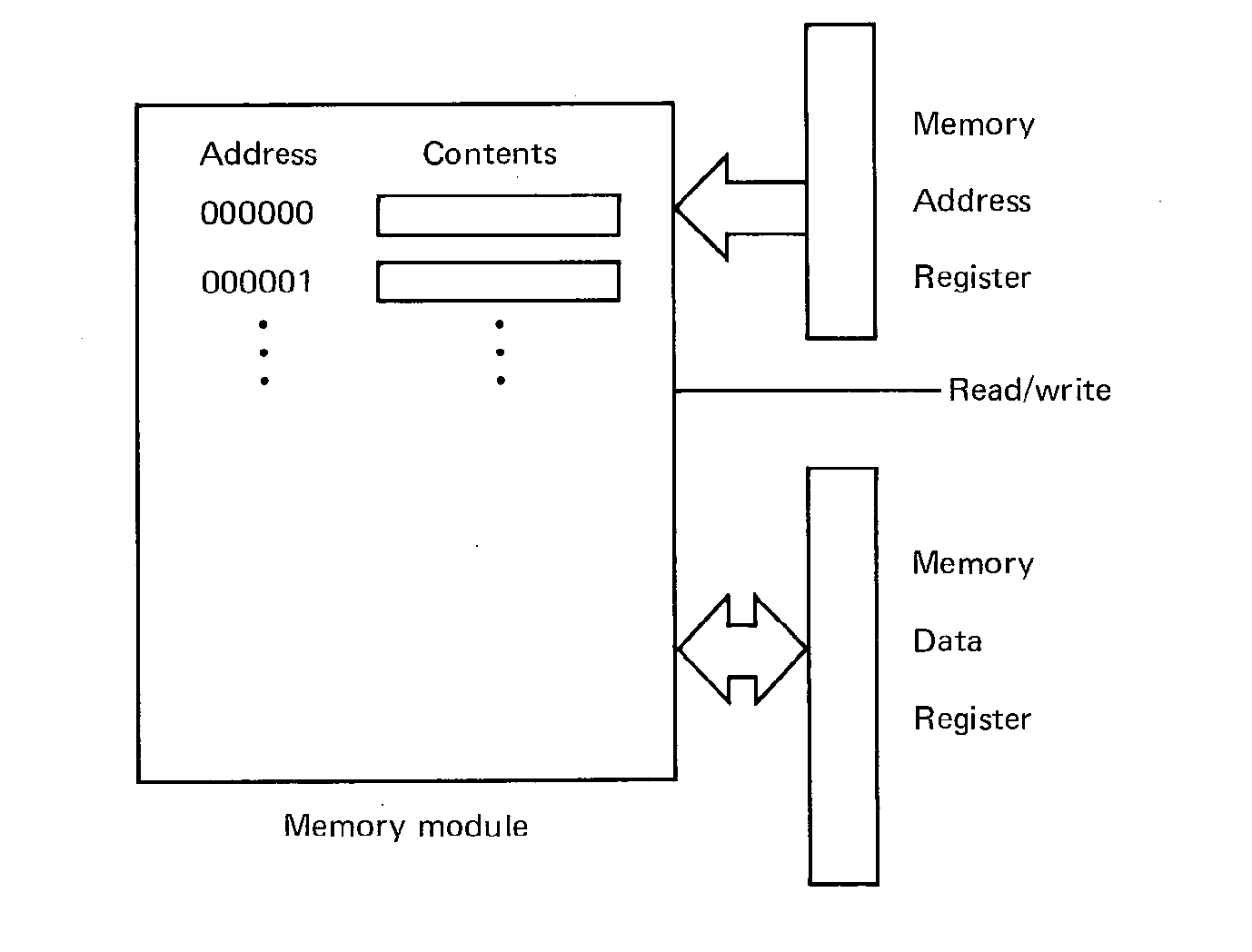FIGURE 1.5 Memory module appearance to rest of system.
The basic element in a core memory is the core. The parameters of the core define the parameters of the memory. Specifically, the size of the core determines its switching time, and switching time defines access time and cycle time. To achieve faster memories, it is necessary to make the cores smaller and smaller. There is a practical limit, given current manufacturing techniques, to the size, and hence, speed, of core memories.
Semiconductor memories use electrical rather than magnetic means to store information. The basic element of a semiconductor memory is often called a flip-flop. Like the core, it has two basic states: on/off, or 0/1, or +/-, and so on. The basic idea is to replace the magnetic cores of a memory with the electrical flip-flops. However, the functional view of memory is the same. Each memory module has a memory address register, a memory data register, and a read-write function selector. The difference lies in how the information is stored in the memory module. Many different kinds of semiconductor memories have been developed.
Bipolar memories are the fastest memories available, with switching times as low as 100 nanoseconds (10-7 seconds). MOS (metallic-oxide semiconductor) memories are slower (500 to 1000 nanoseconds) but cheaper. These memories are made on "chips" which correspond roughly to a core plane. Memory modules are constructed by placing a number of chips on a memory board.
One major problem with semiconductor memories is the volatility of the stored information. In core memories, information is stored magnetically, while semiconductor memories store information electrically. If the power to a semiconductor memory is turned off, the contents of the memory are lost. This means that power is never intentionally turned off, unless all useful information has been stored elsewhere. However, if power is cut off due to an accident, a power failure, or a "brown-out," the consequences can be a major catastrophe. A temporary alternate power supply (such as a battery) can solve this problem, and most systems now have this protection.
Another form of this same volatility exhibits itself in some semiconductor memories. Static memories use transistor-like memory elements which store information by the "on" or "off" state of the transistor. Dynamic memories store information by the presence or absence of an electrical charge on a capacitor. The problem is that the electrical charge will leak off over time, and so dynamic memories must be refreshed at regular intervals. Refreshing a memory requires reading every word and writing it back in place. Special circuitry is used to constantly refresh a dynamic memory.
Almost the opposite of a dynamic memory is a read-only memory (ROM). Read-only memories are very static. In fact, as their name implies, they cannot be written (except maybe the first time, and even that is often difficult). Read-only memories are used for special functions; information is stored once and never changed. For example, read-only memories are often used to store bootstrap loaders (Chapter 7) and interpreters (Chapter 9), programs which are supplied with the computer and are not meant to ever be changed. Most hand calculators are small computers with a special program, stored in ROM, which is executed over and over.
Some read-only memories can in fact be rewritten, but while access time for reading may be only 100 nanoseconds, writing may take several microseconds. These memories are called programmable read-only memories (PROMs) and electrically programmable read-only memories (EPROMs), among others.
Even more advanced forms of semiconductor memories which may be used in the near future include magnetic bubbles and charge-coupled devices (CCDs). The important fact about all of these forms of memory, however, is that despite their various types of physical construction, their interface to the rest of the computer system is the same: an address register, a data register, and a read-write signal. Memory modules can be constructed in many different ways and with many different materials: cores, semiconductors, thin magnetic films, magnetic bubbles, and so on. However, because of the uniform and simple interface to the rest of the computing system, we need not be overly concerned with the physical organization of the memory unit. We need only consider its logical organization.
All (current) computer memories are composed of basic units which can be in either of two possible states. By arbitrarily assigning a label to each of these two states, we can store information in these memory devices. Traditionally, we assign the label 0 to one of these states and 1 to the other state. The actual assignment is important only to the computer hardware designers and builders. We do not care if a 0 is assigned to a clockwise magnetized core and 1 to a counterclockwise magnetized core, or vice versa. What we do want is that if we say to write a 1 into a specific cell, then a subsequent read of that cell returns a 1, and if we write a 0, we will then read a 0. We can then consider memory to store 0s and 1s and may ignore how they are physically stored.
Each 0 or 1 is called a binary digit, or a bit. Each bit can be either a 0 or a 1. A word is a fixed number of bits. The number of bits per word varies from computer to computer. Some small computers have only 8 bits per word, while others have as many as 64 bits per word. Typical numbers of bits per word are 12, 16, 18, 24, 32, 36, 48, and 60, with 16 and 32 being the most common. Each word of memory has an address. The address of a word is the bit pattern which must be put into the memory address register in order to select that word in the memory module. In general, every possible bit pattern in the memory address register will select a different word in memory. Thus, the maximum size of the memory unit (number of different words) depends upon the size of the memory address register (number of bits).
If there are n bits in the memory address register, how many words can there be in memory? With only one bit (n = 1), there are only two possible addresses: 0 and 1. With two bits, there are four possible addresses: 00, 01, 10, and 11. If we have three bits, there are eight possible addresses: 000, 001, 010, 011, 100, 101, 110, and 111. In general, every additional bit in the memory address register doubles the number of possible addresses, so with n bits there are 2n possible addresses. Table 1.1 gives some typical memory sizes and the number of bits in the memory address register.
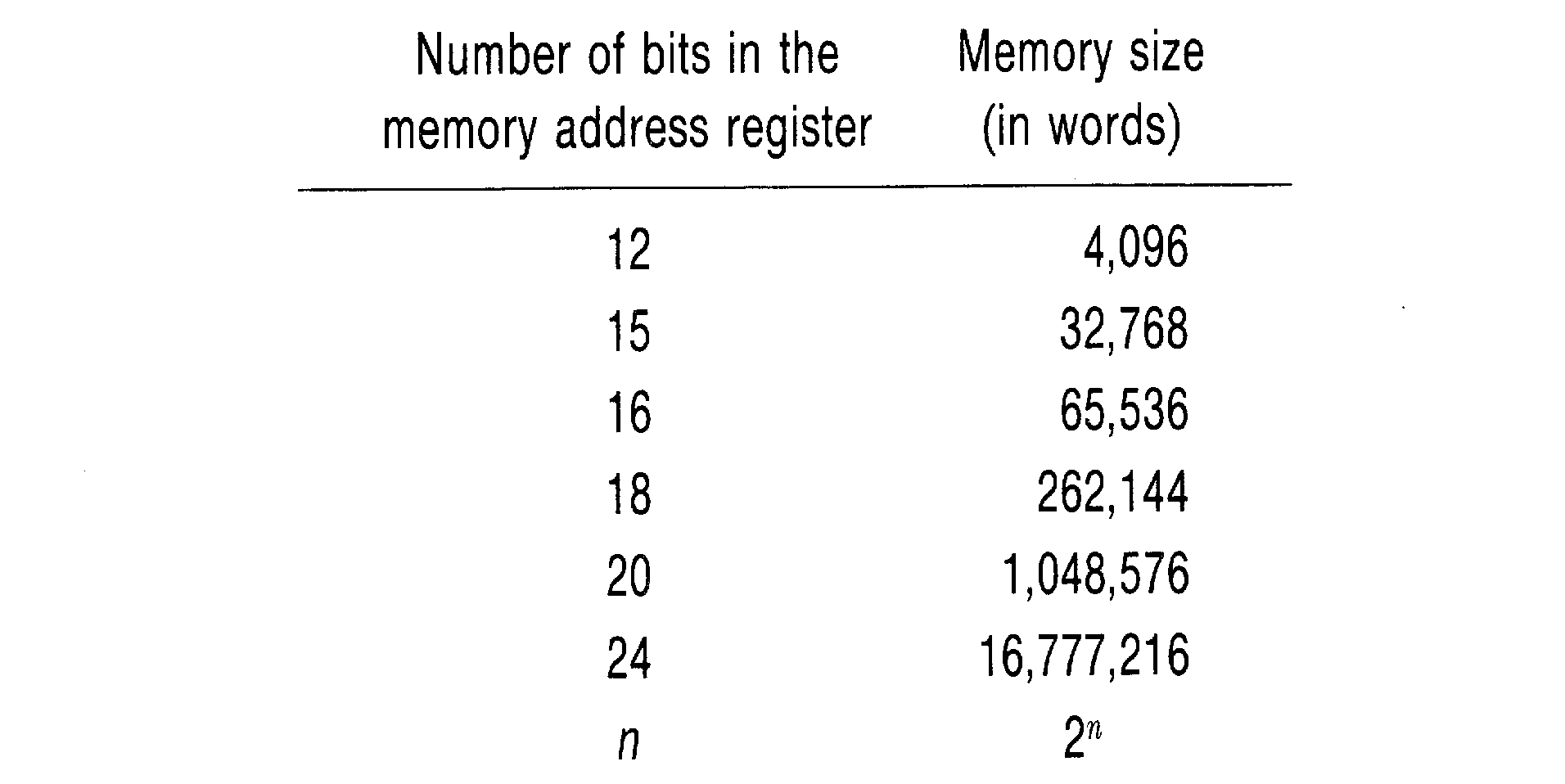
Consider a computer with a 32-bit word and a 16-bit address. This computer could have up to 65,536 different 32-bit words. The purchaser of the computer may not have been able to afford to buy all 65,536 words, however. Memory modules are generally made in sizes of 4096, 8192, 16,384 or 32,768 words. Since 210 = 1024 is almost 1000, these are often referred to as 4K, 8K, 16K, or 32K memories. (The K stands for kilo, meaning 1000. The next size of memory, containing 65,536 words, is referred to as either 64K or 65K.) To get a larger memory, several modules are purchased and combined to form the memory unit. For example, a 64K memory may be made up of four 16K memory modules. The address size for a specific computer only places an upper limit on the amount of memory which can be attached to the computer.
An n-bit word can be drawn as
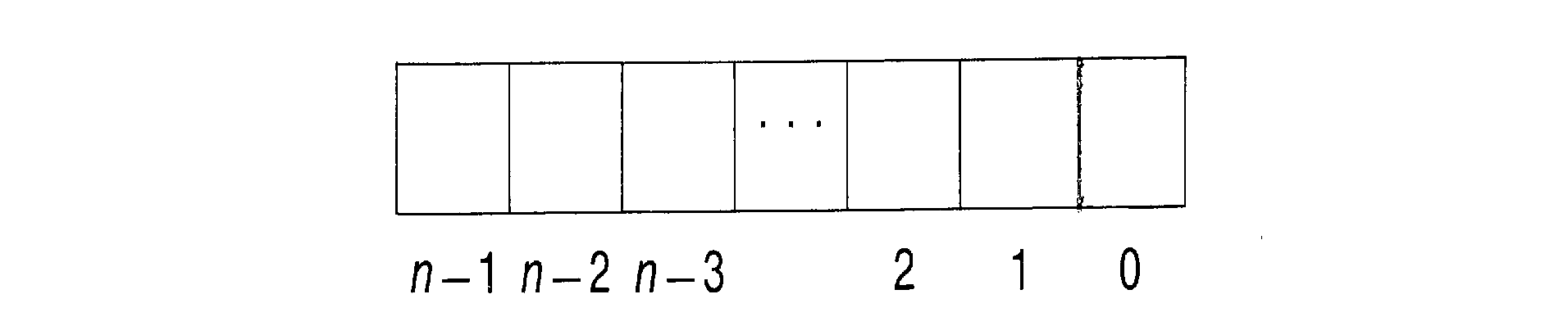To be able to refer to specific bits, we number them. Different
people number their bits differently. Some number from left to
right, others from right to left. Some number their bits from 0
to n-1, others from 1 to n. We will number our
bits from 0 to n-1 from right to left. This will be
convenient in Section 1.2 when
we discuss number systems. The right-hand bits are called
the low-order bits, while the left-hand bits are
called high-order bits.
Many computers consider their words to be composed of bytes. A byte is a part of a word composed of a fixed number (usually 6 or 8) of bits. A 32-bit word could be composed of four 8-bit bytes. These would be bits 0-7, 8-15, 16-23, and 24-31. The usefulness of byte-sized quantities will become apparent in Section 1.3, when we discuss I/O and character codes.
In addition to the words of the memory unit, a computer will probably have a small number of high-speed registers. These are generally either the same size as a word of memory or the size of an address. Most registers are referred to by a name, rather than an address. For example, the memory address register might be called the MAR, and the memory data register the MDR. Typical other registers may include an accumulator (A register) of the computation unit, and the program counter (P register) of the control unit. These registers provide memory for the computer, but they are used for special purposes.
Memory for a computer consists of a large number of fixed-length words. Each word is composed of a fixed number of bits. Words can be stored at specific locations in the memory unit and later read from that location. Each location in memory is one word and has its own unique address. A machine with n-bit addresses can have up to 2n different memory locations.
The computation unit contains the electronic circuitry which manipulates the data in the computer. It is here that numbers are added, subtracted, multiplied, divided, and compared. The computation unit is commonly called the arithmetic and logic unit (ALU).
Since the main function of the computation unit is to manipulate numbers, the design of the computation unit is determined mainly by the way in which numbers are represented within the computer. Once the scheme for representing numbers has been decided upon, the construction of the computation unit is an exercise in electronic switching theory.
Mathematicians have emphasized that a number is a concept. The concept of a specific number can be represented by a numeral. A numeral is simply a convenient means of recording and manipulating numbers. The specific manner in which numbers are represented has varied from culture to culture and from time to time. Early representations of numbers by piles of sticks gave way to making marks in an organized manner (|, ||, |||, ||||, |||||, …). This method in turn eventually was replaced by Roman numerals (I, II, III, IV, V, …) and finally by Arabic numerals (1, 2, 3, 4, 5, …). Notice that we have Roman numerals and Arabic numerals, not Roman numbers or Arabic numbers. The symbols which are used to represent numbers are called digits.
The choice of a number system depends on many things. One important factor is the convenience of expressing and operating on the numerals. Another important idea is the expressive power of the system (Roman numerals, for example, have no representation for zero, or for fractions). A third determining factor is convention. A representation of a number is used both to remember numbers and to communicate them. In order for the communication to succeed, all parties must agree on how numbers are to be represented.
Computers, of course, have only two symbols which can be used as digits. These two digits are the 0 and the 1 symbols which can be stored in the computer's memory unit. We are limited to representing our numbers only as combinations of these symbols. Remember that with n bits we can represent 2n different bit patterns. Each of these bit patterns can be used to represent a different number. (If we were to use more than one bit pattern to represent a number, or one bit pattern to represent more than one number, using the numbers might be more difficult.)
The correspondence between numbers and bit patterns can be quite arbitrary. For example, to represent the eight numbers 0, 1, …, 7, we could use
| Number | Bit pattern |
|---|---|
| | |
| 0 | 110 |
| 1 | 101 |
| 2 | 001 |
| 3 | 100 |
| 4 | 010 |
| 5 | 111 |
| 6 | 011 |
| 7 | 000 |
We are defining a mapping, R, from bit patterns to numbers. The computation unit must be designed so that the mapping, R, is an isomorphism under the operations of addition, subtraction, multiplication, and division, and under relations such as "less than", "equal to", and "greater than". This means that if a bit pattern X and a bit pattern Y are presented to the computation unit for addition and the bit pattern Z is the result, then we want R(X) + R(Y) = R(Z). That is, the number R(Z), represented by the bit pattern Z, should be the sum of the number R(X), represented by the bit pattern X, and the number R(Y), represented by the bit pattern Y.
This requirement, plus the desire to keep the cost of the computer down, has resulted in almost all computers representing their numbers in a positional notation. Everyone should be familiar with positional (or place) notation from our familiar decimal (base 10) number system. In a positional notation, the value of a digit depends upon its place in the numeral. For example, the digit 2 has different values in the three numbers 274, 126, and 592, meaning two hundreds, two tens, and two units, respectively.
In a binary (base 2) place notation, the concepts are the same, but each place can have only two possible digits, 0 or 1, rather than ten (0 through 9) as in the decimal (base 10) place notation. Because of this, the value of the places increases more slowly than with the decimal system. Each place is worth only twice the value of the place to its right, rather than ten times the value as in the decimal system. The rightmost place represents the number of units; the next rightmost, the number of "twos"; the next, the number of "fours"; and so forth. Counting in the binary positional number system proceeds
| 0, | 1, | 10, | 11, | 100, | 101, | 110, | 111, | 1000, | 1001, | … |
| 0, | 1, | 2, | 3, | 4, | 5, | 6, | 7, | 8, | 9, | … |
We stopped at 9 above, because at 10 two major methods of representing numbers in a computer show their differences. One method, the binary system (discussed in the following section), continues as above. The other system, the decimal system uses the above bit patterns to represent the digits from 0 to 9, and then uses these digits to represent all other numbers. The decimal system represents numbers in the familiar decimal place system, replacing the digits 0 through 9 with 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, respectively. This is known as a binary coded decimal (BCD) representation. For example, the numbers 314,159 and 271,823 are represented in BCD by
| 314,15910 | = | 0011 | 0001 | 0100 | 0001 | 0101 | 1001BCD |
| 271,82310 | = | 0010 | 0111 | 0001 | 1000 | 0010 | 0011BCD |
To add these numbers, we add each digit of the addend to the corresponding digit of the augend to give the sum digit. Each digit is represented in binary, so binary arithmetic is used. For binary addition, the addition table is
| 0 | + | 0 | = | 0 |
| 1 | + | 0 | = | 1 |
| 0 | + | 1 | = | 1 |
| 1 | + | 1 | = | 0 with a carry into the next higher place |
| 0011 | 0001 | 0100 | 0001 | 0101 | 1001 | (BCD) | |
| + | 0010 | 0111 | 0001 | 1000 | 0010 | 0011 | (BCD) |
| | | | | | | ||
| 0101 | 1000 | 0101 | 1001 | 0111 | 1100 | (BCD) |
| 0101 | 1000 | 0101 | 1001 | 0111 | 1100 | (BCD) | |
| +0001 | -1010 | (correction) | |||||
| | | | | | | ||
| 0101 | 1000 | 0101 | 1001 | 1000 | 0010 | (BCD) |
| 314,159 | |
| + | 271,823 |
| | |
| + | 585,982 |
The decimal number system has been used in many computers, particularly the earlier machines. It has several distinct advantages over competing number systems. Its greatest advantage is its similarity to the representation of numbers used by most people. Numbers can be easily read into the machine and output again. Its major disadvantages tend to outweigh these considerations, however. Compared to the binary number systems which we discuss next, the computation unit circuitry for addition, and so forth, is much more complicated (and hence more expensive). Furthermore, it uses only 10 of the 16 possible bit patterns in 4 bits (24 = 16), so that it wastes memory. To represent the numbers from 0 to 99,999,999 would take 32 bits (4 bits per digit times 8 digits) in BCD, while only 27 bits provide many more than 100,000,000 different bit patterns (227 = 134,217,728). At $.05 per bit, this means each word costs ($.05 per bit times 5 bits) $.25 more for decimal than for binary, and a memory module of 4096 words would cost an extra thousand dollars.
For certain applications, however, these considerations are not as important. An electronic calculator, for example, normally uses a decimal number representation scheme, since a calculator uses very little memory, but must be compatible with human operators. Also, as the price of computer memory and logic hardware decreases, so will the cost disadvantage of decimal machines.
In the binary number system, numbers are represented by a sequence of binary digits (bits). Each bit has a value determined by its position in the number. The sequence of bits
| Xn Xn-1 … X2 X1 X0 | 0 ≤ Xi ≤ 1 |
| X0 + 2 × X1 + 4 × X2 + 8 × X3 + … + 2n-1 × Xn-1 + 2n × Xn |
| Binary number | Decimal number |
|---|---|
| | |
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
| 10000 | 16 |
| 10001 | 17 |
| 10010 | 18 |
| … | … |
The largest number which can be represented in n bits is 111…111 (n bits of 1) which is
| 1 + 2 + 4 + 8 + … + 2n-1 | = | 2n - 1 |
Binary arithmetic is quite simple. The addition table is simply
| 0 | + | 0 | = | 0 |
| 1 | + | 0 | = | 1 |
| 0 | + | 1 | = | 1 |
| 1 | + | 1 | = | 0 with a carry of 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | carries | ||||||||
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | addend | |
| + | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | augend |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | sum |
| 1 | 1 | 1 | 1 | 1 | carries | ||||||||||||
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | addend | |
| + | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | augend |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | sum |
The hardware to build a computational unit for a binary machine is quite simple and easy to design and build. The major disadvantage with binary systems is their inconvenience and unfamiliarity to humans (Quick! Is 010101110010 [base 2] greater or less than 1394 [base 10]?). The large number of symbols (zeros and ones) which must be used to represent even "small" numbers is also cumbersome. Hence, very few programmers prefer to work in binary. But the computer must work completely in binary. It has no choice, due to the binary nature of computer hardware. What is needed is a quick and easy way to convert between binary and decimal. Unfortunately, there is no quick and easy conversion algorithm between these two bases.
In an arbitrary base B (B > 0) a sequence of digits
| Xn Xn-1 … X2 X1 X0 | (0 ≤ Xi < B) |
| X0 + B × X1 + B2 × X2 + … + Bn-1 × Xn-1 + Bn × Xn |
To convert from binary to decimal, we use the equation given above to calculate the decimal representation of the binary number. For example,
| 0110101001 (base 2) | = | 0 × 29 + 1 × 28 + 1 × 27 + 0 × 26 + 1 × 25 |
| + 0 × 24 + 1 × 23 + 0 × 22 + 0 × 21 + 1 × 20 | ||
| = | 0 × 512 + 1 × 256 + 1 × 128 + 0 × 64 + 1 × 32 | |
| + 0 × 16 + 1 × 8 + 0 × 4 + 0 × 2 + 1 × 1 | ||
| = | 256 + 128 + 32 + 8 + 1 | |
| = | 433 (base 10) | |
| 1000101100 (base 2) | = | 1 × 29 + 1 × 25 + 1 × 23 + 1 × 22 |
| = | 512 + 32 + 8 + 4 | |
| = | 556 (base 10) |
| n | 2n | |
|---|---|---|
| | | |
| 0 | 1 | |
| 1 | 2 | |
| 2 | 4 | |
| 3 | 8 | |
| 4 | 16 | |
| 5 | 32 | |
| 6 | 64 | |
| 7 | 128 | |
| 8 | 256 | |
| 9 | 512 | |
| 10 | 1,024 | |
| 11 | 2,048 | |
| 12 | 4,096 | |
| 13 | 8,192 | |
| 14 | 16,384 | |
| 15 | 32,768 | |
| 16 | 65,536 | |
| 17 | 131,072 | |
| 18 | 262,144 | |
| 19 | 524,288 | |
| 20 | 1,048,576 | |
| 21 | 2,097,152 | |
| 22 | 4,194,304 | |
| 23 | 8,388,608 | |
| 24 | 16,777,216 | |
| 25 | 33,554,432 |
To convert from decimal to binary requires a different approach. For a number x, we have the equation
| x | = | X0 + 2 × X1 + 4 × X2 + 8 × X3 + … + 2n-1 × Xn-1 + 2n × Xn |
| Xn Xn-1 … X2 X1 X0 | 0 ≤ Xi ≤ 1 |
| x | = | X0 + 2 × (X1 + 2 × (X2 + 2 × (X3 + … + 2 × (Xn-1 + 2 × Xn) … ))) |
| 47132 ÷ 2 | = | 23566 | remainder is 0 |
| 23566 ÷ 2 | = | 11783 | remainder is 0 |
| 11783 ÷ 2 | = | 5891 | remainder is 1 |
| 5891 ÷ 2 | = | 2945 | remainder is 1 |
| 2945 ÷ 2 | = | 1472 | remainder is 1 |
| 1472 ÷ 2 | = | 736 | remainder is 0 |
| 736 ÷ 2 | = | 368 | remainder is 0 |
| 368 ÷ 2 | = | 184 | remainder is 0 |
| 184 ÷ 2 | = | 92 | remainder is 0 |
| 92 ÷ 2 | = | 46 | remainder is 0 |
| 46 ÷ 2 | = | 23 | remainder is 0 |
| 23 ÷ 2 | = | 11 | remainder is 1 |
| 11 ÷ 2 | = | 5 | remainder is 1 |
| 5 ÷ 2 | = | 2 | remainder is 1 |
| 2 ÷ 2 | = | 1 | remainder is 0 |
| 1 ÷ 2 | = | 0 | remainder is 1 |
A different algorithm can be used when a table of the powers of two (such as Table 1.2) can be used. Suppose we want to convert 747 (base 10) to binary. Looking in the table, we see that the first power of two that is less than 747 is 512 (= 29). Since 747 - 512 = 235, we can construct the following sequence
| 747 (base 10) | = | 512 + 235 |
| = | 512 + 128 + 107 | |
| = | 512 + 128 + 64 + 43 | |
| = | 512 + 128 + 64 + 32 + 11 | |
| = | 512 + 128 + 64 + 32 + 8 + 3 | |
| = | 512 + 128 + 64 + 32 + 8 + 2 + 1 | |
| = | 29 + 27 + 26+ 25 + 23 + 21+ 20 | |
| = | 1011101011 (base 2) |
As we said earlier, there is no conversion method between binary and decimal that is so quick and simple that it can be done in your head. A simple observation leads, however, to two reasonable alternatives to using binary. Consider the expansion of the 12-bit binary number
| x | = | X11X10X9X8 … X2X1X0 | ||
| = | X0 + 2 × X1 + 4 × X2 + 8 × X3 + 16 × X4 + 32 × X5 | |||
| + | 64 × X6 + 128 × X7 + 256 × X8 + 512 × X9 + 1024 × X10 + 2048 × X11 | [1] | ||
| = | (X0 + 2 × X1 + 4 × X2) | |||
| + | 8 × (X3 + 2 × X4 + 4 × X5) | |||
| + | 82 × (X6 + 2 × X7 + 4 × X8) | |||
| + | 83 × (X9 + 2 × X10 + 4 × X11) | [2] | ||
| = | (X0 + 2 × X1 + 4 × X2 + 8 × X3) | |||
| + | 16 × (X4 + 2 × X5 + 4 × X6 + 8 × X7) | |||
| + | 162 × (X8 + 2 × X9 + 4 × X10 + 8 × X11) | [3] |
| x | = | 80 × Y0 + 81 × Y1 + 82 × Y2 + 83 × Y3 |
| x | = | 160 × Z0 + 161 × Z1 + 162 × Z2 |
As a direct result of the fact that 8 = 23 and 16 = 24 we can easily convert between binary and octal or binary and hexadecimal. To convert a binary number to octal, start at the right-hand side (low-order bits) and group the bits, three bits per group. Add leading zeros as necessary to make the number of bits a multiple of three. To convert to hexadecimal, group four bits per group, with leading zeros as necessary to make the total number of bits a multiple of four. Then convert each group as follows.
| Binary | Octal | Binary | Octal | ||
|---|---|---|---|---|---|
| | | | | ||
| 000 | 0 | 100 | 4 | ||
| 001 | 1 | 101 | 5 | ||
| 010 | 2 | 110 | 6 | ||
| 011 | 3 | 111 | 7 |
| Binary | Hexadecimal | Binary | Hexadecimal | ||
|---|---|---|---|---|---|
| | | | | ||
| 0000 | 0 | 1000 | 8 | ||
| 0001 | 1 | 1001 | 9 | ||
| 0010 | 2 | 1010 | A (10) | ||
| 0011 | 3 | 1011 | B (11) | ||
| 0100 | 4 | 1100 | C (12) | ||
| 0101 | 5 | 1101 | D (13) | ||
| 0110 | 6 | 1110 | E (14) | ||
| 0111 | 7 | 1111 | F (15) |
As an example of the conversion from binary to octal,
consider 111000110010100110 and 11110011010111001010
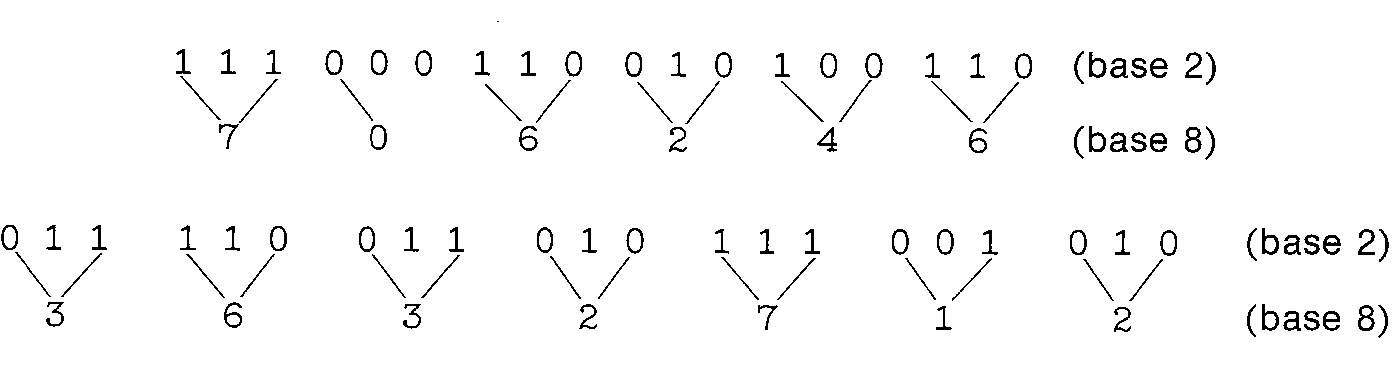In this last case, we have added a leading zero in
order to convert from binary to octal. For conversion to hexadecimal we
have,
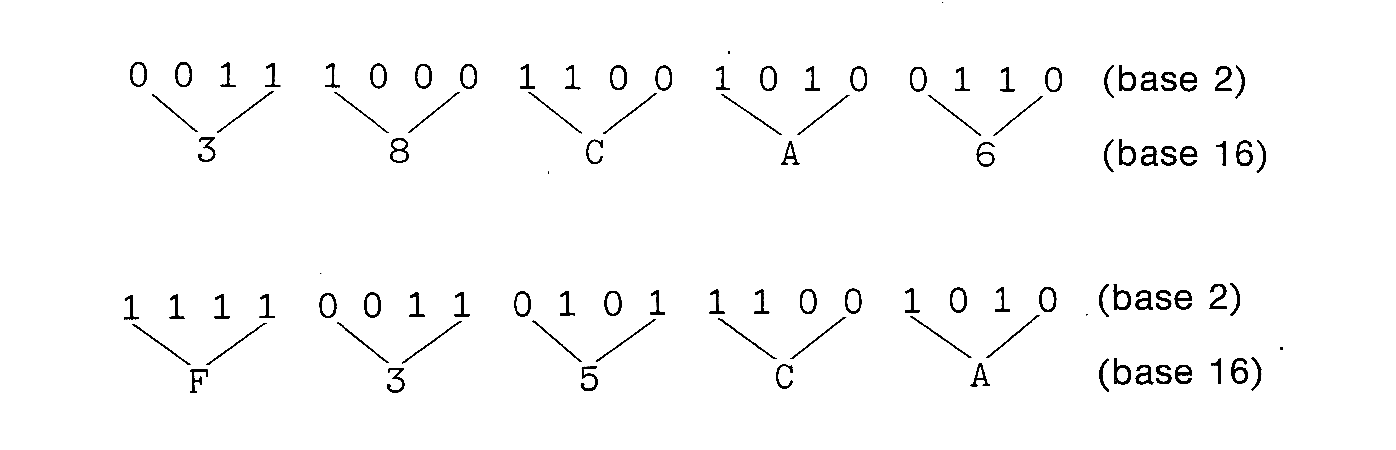
Conversion from hexadecimal to binary or from octal to
binary is simply the reverse of the above transformation.
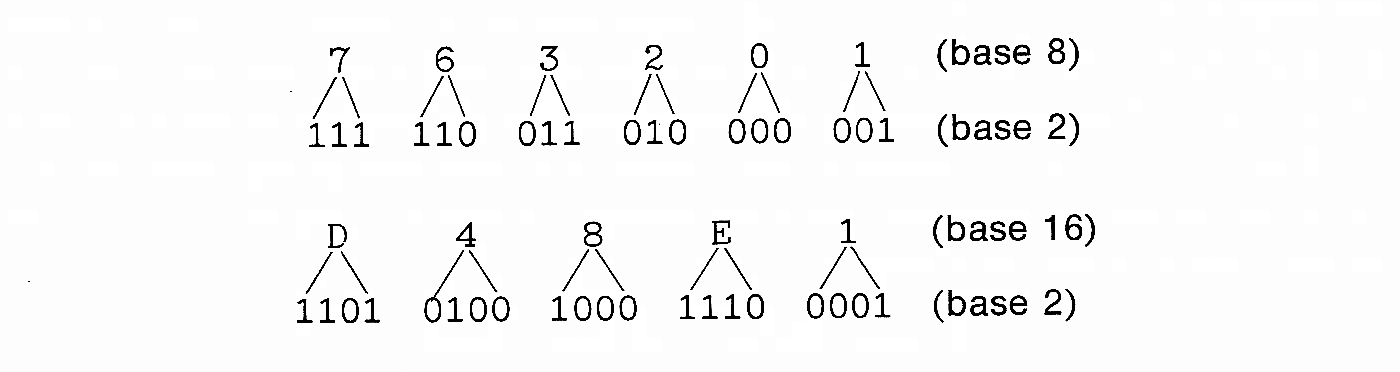
Because these conversions can be done easily and quickly, bit patterns are almost never given in binary, but in octal or hexadecimal. Addition in these systems is basically the same as in base 10, except that carries occur whenever a sum exceeds 8 (in octal) or 16 (in hexadecimal).
The choice between using octal or hexadecimal is largely a matter of personal taste. There are some objective measures which can be used to compare them. Hexadecimal obviously will use fewer characters to represent a bit string. For a 32-bit number, for example, only 8 hexadecimal digits are needed, while 11 octal digits would be necessary. Machine word lengths (the number of bits per word) tend to be powers of 2, and 4 bits per hexadecimal digit gives an integral number of hexadecimal digits per word, in these cases. Thus, for machines with word lengths of 12, 16, 24, 32, 48, 60, or 64 bits, hexadecimal is a convenient choice.
Octal, on the other hand, has the advantage of being "closer" to base ten than hexadecimal. Machines with 12, 18, 24, 36, 48, or 60 bits per word have an integral number of octal digits per word. Only eight conversions between octal and binary need to be memorized (as opposed to 16 for hexadecimal). Also, all octal digits are decimal digits, so octal numbers look like numbers (not like half-word, half-number hybrids). Still, this means octal can be mistaken for decimal, while a hexadecimal number is more likely to have a digit which is not a decimal digit.
Most decisions to use either octal or hexadecimal as the primary way to represent binary numbers are determined by personal bias. We use octal, in this text.
One advantage of octal mentioned above was that it was "close" to base 10. This can be very useful when quick order-of-magnitude type comparisons are needed with binary numbers and decimal numbers. Table 1.3 gives a short table of octal numbers and their decimal equivalents. Notice that until about 1000 (octal) = 512 (base 10), octal numbers and decimal numbers are very similar in magnitude. Even with 18-bit numbers, octal numbers are only about 4 times smaller than they should be. Hence, a very crude way to interpret a binary number is to convert it to octal, and then treat that octal number as a decimal number.
| | | | | ||
| Octal | Decimal | Octal | Decimal | ||
| | | | | ||
| 10 | 8 | 1 000 | 512 | ||
| 40 | 32 | 4 000 | 2,048 | ||
| 100 | 64 | 10 000 | 4,096 | ||
| 200 | 128 | 100 000 | 32,768 | ||
| 400 | 256 | 1 000 000 | 262,144 |
Of course, this crude conversion gives only order-of-magnitude results. To know exactly the value of an octal number, we need to follow the same multiplicative algorithm which we saw earlier for base 2, but now we are working with base 8, so the multiplicative factor is eight. For example
| 1742 (octal) | = | 1 × 83 + 7 × 82+ 4 × 8 + 2 × 1 |
| = | 512 + 448 + 32 + 2 | |
| = | 994 (base 10) |
| 40653 (octal) | = | 4 × 84 + 0 × 83 + 6 × 82 + 5 × 8 + 3 × 1 |
| = | 16384 + 0 + 384 + 40 + 3 | |
| = | 16811 (base 10) |
| Digit position | ||||||
| Digit | 6 | 5 | 4 | 3 | 2 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 32768 | 4096 | 512 | 64 | 8 | 1 |
| 2 | 65536 | 8192 | 1024 | 128 | 16 | 2 |
| 3 | 98304 | 12288 | 1536 | 192 | 24 | 3 |
| 4 | 131072 | 16384 | 2048 | 256 | 32 | 4 |
| 5 | 163840 | 20480 | 2560 | 320 | 40 | 5 |
| 6 | 196608 | 24576 | 3072 | 384 | 48 | 6 |
| 7 | 229376 | 28672 | 3584 | 448 | 56 | 7 |
A different method of conversion is to express the original equation of a conversion as
| x | = | X0 + B1 × X1 + B2 × X2 + B3 × X3 + … + Bn × Xn |
| = | X0 + B × (X1 + B × (X2 + B × (X3 + … + B × Xn …))) |
Using this form of the conversion equation, we can convert 3756 (octal) to decimal by
| 3756 (octal) | = | 6 + 8 × (5 + 8 × (7 + 8 × 3)) |
| = | 6 + 8 × (5 + 8 × 31) | |
| = | 6 + 8 × 253 | |
| = | 2030 (base 10) |
To convert back from decimal to octal, we repeatedly divide the decimal number by 8. The remainder at each step is the octal digit, with low-order digits produced first. Thus, converting 2030 (base 10) to octal gives
| 2030 ÷ 8 | = | 253, | remainder = 6 |
| 253 ÷ 8 | = | 31, | remainder = 5 |
| 31 ÷ 8 | = | 3, | remainder = 7 |
| 3 ÷ 8 | = | 0, | remainder = 3 |
Similar algorithms can be used to convert between decimal and hexadecimal.
Now that we are familiar with the use of the different number systems, how do we use this information to represent numbers in the computer? A number is represented by setting the bits in a word of the computer memory to the binary representation of the number. To perform arithmetic operations on two numbers (for example, to add them), the words containing the binary representation of the two numbers are read from memory, or registers, and copied to the computation unit. The computation unit is instructed (by the control unit) as to which operation is to be performed, and when the operation is complete the result is stored back in memory or a register.
The different operations which the computation unit may be asked to do vary from computer to computer, but almost every computer can at least add two numbers. Like reading or writing information in memory, the operations done by the computation unit take time. Generally the computation unit operates somewhat faster than the memory cycle time. The time to do an addition (the add time) varies from machine to machine due to different hardware designs and components, and also due to different word lengths. Longer words mean longer waiting for carries to propagate. Add times typically are from 0.3 to 2 microseconds.
Addition of two n-bit words may produce a number requiring n + 1 bits for its representation. This is too large to fit into one computer word and is known as overflow. For example, if we were working with a 6-bit computer word, we could represent the numbers from 000000 (base 2) (00 (octal) = 0 (base 10)) up to 111111 (base 2) (77 (octal) = 63 (base 10)). If we add 010110 (base 2) (26 (octal)) to 100101 (base 2) (45 (octal)), we have a sum of
| 0 | 1 | 0 | 1 | 1 | 0 | (26 (octal)) | |
| 1 | 0 | 0 | 1 | 0 | 1 | (45 (octal)) | |
| 1 | 1 | 1 | 0 | 1 | 1 | (73 (octal)) | |
| 1 | 0 | 1 | 0 | 1 | 0 | (52 (octal)) | |
| 1 | 1 | 0 | 0 | 0 | 1 | (61 (octal)) | |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | |
Subtraction of binary numbers is similar to addition, except that we may generate a "borrow" of 1 from the next higher place rather than a "carry". For example
| 0 | 10 | (borrows) | |||||
| 1 | 0 | 0 | 1 | 1 | 1 | (47 (octal)) | |
| - | 0 | 1 | 0 | 1 | 0 | 1 | (25 (octal)) |
| 0 | 1 | 0 | 0 | 1 | 0 | (22 (octal)) | |
The possibility of subtraction brings up the problem of the representation of negative numbers. So far we have considered only the problem of representing positive numbers, and have seen that there are at least two methods of representation: decimal and binary. Negative numbers may also be stored and manipulated in the computer as well. Several methods of representing negative numbers, in addition to positive numbers, are used in computers. We consider here four representation schemes
In the early designs of computers the representation of numbers was in BCD because the algorithms for decimal arithmetic were familiar to the designers, builders, and users of the computer. For much the same reasons, a sign and magnitude representation of negative numbers was used. To represent positive and negative numbers, all we need is a sign (+ or -) and the absolute value of the number (its magnitude). Thus, positive 5 is represented by +5 and negative 5 by -5. The same scheme can be used in binary, octal, decimal, or any other number system. Positive 100110 (base 2) is represented by +100110 (base 2) and negative 100110 (base 2) is represented by -100110 (base 2). The sign can be represented by encoding a plus (+) as a 0 and a minus (-) as a 1 and attaching this sign bit to the front of the word. The decision to make plus a 0 bit, and minus a 1 bit is arbitrary, but was done to represent zero by 00…000. An n-bit word has a high-order sign bit and n-1 bits to represent the magnitude of the number. The range of numbers which can be represented is
| -2n-1+1, …, 0, …, +2n-1-1 |
Notice that this method of specifying negative numbers can also be used for a BCD representation of numbers. To represent the numbers from -999,999,999 (base 10) to +999,999,999 (base 10), we would use a 1-bit sign bit and 9 BCD digits of 4 bits each, so our word length would be 37 bits.
A quirk of sign and magnitude for binary numbers is the existence of 100…000 as a signed number. The sign bit is 1, so the number has a negative sign, but the magnitude is zero. This number is known as minus zero (-0) or negative zero, and is the negative of positive zero (+0).
The major problem with sign and magnitude notation, however, is the complexity of the computational unit necessary to operate on sign and magnitude numbers. If we wish to add two numbers, we must first examine their signs, and if they differ, subtract one from the other rather than adding. This means we must have both adding and subtracting devices (adders and subtracters) in our computation unit. These units are very similar in design, so this may double the cost of the computation unit, over those with only adders. If we could find an easy way to simply add two numbers, rather than having to subtract for different signs, and a way to find the negative of a number, then we could utilize the fact that x - y = x + (-y) and dispense with the subtracter (or the adder, since x + y = x - (-y)).
Ones' complement notation was devised to make the adding of two numbers with different signs the same as for two numbers with the same sign. The complement of a binary number is the number which results from changing all 0s to 1s and all 1s to 0s in the original number. For example, in a 12-bit machine, the complement of 0110100111010011 is 1001011000101100, and the complement of 1110111101011011 is 0001000010100100. The complement of 00…000 is 11…111 and the complement of 11…111 is 00…000. In octal, the complement of each octal digit is
| Complement | Complement | ||
|---|---|---|---|
| Octal | Binary | Binary | Octal |
| 0 | 000 | 111 | 7 |
| 1 | 001 | 110 | 6 |
| 2 | 010 | 101 | 5 |
| 3 | 011 | 100 | 4 |
| 4 | 100 | 011 | 3 |
| 5 | 101 | 010 | 2 |
| 6 | 110 | 001 | 1 |
| 7 | 111 | 000 | 0 |
To evaluate the usefulness of this scheme for representing negative numbers, consider each of the four possible combinations of signs for adding two numbers, 33 (base 10) and 21 (base 10), in 8-bit binary
| + | 33 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | |||
| + | 21 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| + | 54 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | = 54 (base 10) | ||
| + | 33 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | |||
| - | 21 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | |||
| + | 12 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | = 11 (base 10) plus a carry | |
| - | 33 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |||
| + | 21 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| - | 12 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | = -12 (base 10) | ||
| - | 33 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |||
| - | 21 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | |||
| - | 54 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | = -55 (base 10) plus a carry | |
| + | 33 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | |||
| - | 21 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | |||
| + | 12 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | ||
| + | 1 | end-around carry | ||||||||||
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | = 12 (base 10) | ||||
| - | 33 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |||
| - | 21 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | |||
| - | 54 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | ||
| + | 1 | end-around carry | ||||||||||
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | = -55 (base 10) | ||||
Overflow is still possible, of course, although the method of detecting it is different from the method used for unsigned integers. Before considering overflow, notice that,
Now consider the addition of two positive numbers and two negative numbers which cause overflow. For an 8-bit word (7 bits plus sign), we can represent the range of integers from -127 to +127, so
| + | 100 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | ||||
| + | 28 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | ||||
| + | 128 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | -127 (base 10) | ||
| - | 100 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | ||||
| - | 28 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | ||||
| - | 128 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |||
| + | 1 | end-around carry | |||||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | +127 (base 10) | ||||
Ones' complement allows simple arithmetic with negative numbers. It does suffer from one problem that sign and magnitude notation has: negative zero. The complement of zero (00…000) is negative zero (11…111). Because of the end-around carry, the properties of negative zero are the same as the properties of positive zero, as far as arithmetic is concerned. For example, 307 (octal) + -0 on a 10-bit word is
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |||
| + | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | ||
| + | 1 | end-around carry | ||||||||||
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | = 307 (octal) | ||
To correct the problem of negative zero, two's complement arithmetic is used. The ones' complement arithmetic is fine except for negative zero, so to eliminate it, two's complement notation moves all negative numbers "up" by one. The two's complement negative of a number is formed by complementing all bits and then adding one. The two's complement of 342 (octal) on a 12-bit machine is
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | ||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | complement | |
| + | 1 | plus one | |||||||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | two's complement negative | |
| + | 33 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | |||
| + | 21 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| + | 54 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | = 54 (base 10) | ||
| + | 33 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | |||
| - | 21 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | |||
| + | 12 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | = 12 (base 10) plus a carry | |
| - | 33 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |||
| + | 21 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| - | 12 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | = -12 (base 10) | ||
| - | 33 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |||
| - | 21 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | |||
| - | 54 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | = -54 (base 10) plus a carry | |
Negative zero has disappeared, since
| zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| complement | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| add 1 | + | 1 | ||||||||||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = 0 (discard carry) | |
Overflow is detected in the same way as in ones' complement; if the signs of the inputs are equal, but differ from the sign of the output, or if the carry into the sign differs from the carry out of the sign.
A new "quirk" has appeared to replace minus zero, however. The range of numbers which can be represented in n bits for ones' complement notation is
| -2n-1 + 1 | to | 2n-1 - 1 |
| -2n-1 | to | 2n-1 - 1 |
| -128 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| complement | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| add 1 | + | 1 | ||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = -128 (base 10) | ||
Another scheme for representing negative numbers is excess 2n-1 notation. In this scheme, the range of numbers from -2n-1 to 2n-1 - 1 is represented by biasing each number by 2n-1. Biasing is done by adding the bias (2n-1 in this case) to the number to be biased. This transforms the represented numbers to the range 0 to 2n-1. These biased numbers can be represented in the normal n-bit unsigned binary notation. Excess notation is identical to two's complement notation, but with the sign bit complemented (a 0 sign bit means a negative number, a 1 sign bit a positive number; the opposite of a normal sign bit).
The major advantage of excess notation is with comparisons. For the normal sign bit definition (0 = +, 1 = -), signed and unsigned numbers must be compared differently. If 0100 and 1011 are unsigned integers, then 1011 > 0100, but if they are signed, then 0100 > 1011, since 0100 is positive and 1011 is negative. By reversing the sign bit definition, both signed and unsigned numbers can be compared in the same way, since 1 > 0 and + > -. (On the other hand, the adder now has to treat the sign bit differently from the other bits when addition is being done.)
All of these schemes (sign and magnitude, ones' complement, two's complement, and excess) are used for the representation of numbers in some computer system. They are simply convenient methods of defining the mapping from bit patterns to the integers which we wish to represent in the computer. Different notations assign the bit patterns to suit different purposes. Table 1.5 illustrates how a 4-bit word is interpreted differently for each of the schemes we have discussed. The bit pattern is the same; only the interpretation of its meaning differs. Most computer systems use only one of these methods for representing integers so that the same interpretation can be applied to all words.
| Unsigned | Sign and magnitude | One's complement | Two's complement | Excess 8 | |
| 0000 | 0 | 0 | 0 | 0 | -8 |
| 0001 | 1 | 1 | 1 | 1 | -7 |
| 0010 | 2 | 2 | 2 | 2 | -6 |
| 0011 | 3 | 3 | 3 | 3 | -5 |
| 0100 | 4 | 4 | 4 | 4 | -4 |
| 0101 | 5 | 5 | 5 | 5 | -3 |
| 0110 | 6 | 6 | 6 | 6 | -2 |
| 0111 | 7 | 7 | 7 | 7 | -1 |
| 1000 | 8 | -0 | -7 | -8 | 0 |
| 1001 | 9 | -1 | -6 | -7 | 1 |
| 1010 | 10 | -2 | -5 | -6 | 2 |
| 1011 | 11 | -3 | -4 | -5 | 3 |
| 1100 | 12 | -4 | -3 | -4 | 4 |
| 1101 | 13 | -5 | -2 | -3 | 5 |
| 1110 | 14 | -6 | -1 | -2 | 6 |
| 1111 | 15 | -7 | -0 | -1 | 7 |
Addition and subtraction are two very common operations in a computer, and the computation unit provides the ability to perform these operations on binary numbers. As we hinted earlier, most computers do not provide separate adding and subtracting devices, but only an adder (or subtracter) and a device to complement or negate numbers. This requires that subtraction be done by negation and addition (or that addition be done by negation and subtraction).
Multiplication and division do not occur as frequently as addition and subtraction, so many of the smaller computers do not provide hardware to multiply or divide, but require that the programmer implement multiplication by repeated additions, and division by repeated subtraction. Larger computers, however, do generally provide multiplication and division hardware. Both of these functions normally take more time to perform than addition.
In addition to the increased time required for multiplication, the problem of overflow becomes more important. When two n-bit numbers are added, overflow may occur because the result may generate a carry out of the high-order bit. The largest number which can be represented in an unsigned n-bit number is 2n-1, and so the sum of any two numbers can be no larger than 2n - 1 + 2n - 1 = 2n+1 - 2 which requires n + 1 bits for its representation. For multiplication, the largest possible result is (2n - 1) × (2n - 1) = 22×n - 2n+1 + 1 which requires 2 × n bits, or twice as many bits. In decimal, for example, 99 × 99 = 9801, so the product of two two-digit numbers may be a four-digit number. To represent the entire product, a double-length register is used. This is commonly done by using two single-length registers and considering them as one long register with twice the normal number of bits. If the result of a multiplication is to be used further, with addition, subtraction, or further multiplication, the high-order bits had best be all zeros (or all ones, if the product is negative and represented in ones' complement or two's complement). Otherwise, the product is a number which is too large to be represented in one word of memory and hence cannot be operated on by the normal arithmetic operations.
For division, the opposite phenomenon occurs. A 2 × n-bit dividend divided by an n-bit divisor may result in an n-bit quotient plus an n-bit remainder. For example, the four-digit number 1478 divided by the two-digit number 55 yields the two-digit quotient 26 and the two-digit remainder 48. Thus, many computation units require a double-length dividend and produce two single-length results, the quotient and the remainder. If a single length dividend is desired, it is extended to a double-length representation for the division. For sign and magnitude, this involves simply inserting additional high-order (leading) zeros. For ones' complement, two's complement, and excess notation, this is done by sign extension. The sign bit is replicated as the new high-order bits. For example, in ones' complement, a 6-bit representation of 13 (base 10) is 001101 (base 2), while a 12-bit representation is 000000001101 (base 2). For -13 (base 10), we have 110010 for a 6-bit representation and 111111110010 for a 12-bit representation. Only the high order 6 bits differ between the 6-bit and 12-bit representations, and each of these bits is the same as the sign bit. If the quotient which results from a division exceeds the normal word length, it can be treated either as overflow or as a double-length quotient, according to how the computation unit is built. The remainder of a division by an n-bit divisor is never more than n-bits.
The divide operation discussed above is often called an integer divide, since it divides one integer by another and produces an integer quotient and integer remainder. An alternative way to represent the result would be to give the quotient as a fraction. How do we represent fractions? In common decimal mathematical notation, fractions can be represented in two different forms, as a ratio a/b or as a decimal fraction, 0.xxxx…xx. A decimal fraction is another example of positional notation, but with weights of negative powers of ten (the base) associated with the places. For example
| 0.357 | = | 3 × 10-1 + 5 × 10-2 + 7 × 10-3 |
| 0.1011 (base 2) | = | 1 × 2-1 + 0 × 2-2 + 1 × 2-3 + 1 × 2-4 |
| = | 0.5 + 0.125 + 0.0625 | |
| = | 0.6875 (base 10) |
| 1100.011 (base 2) | = | 1 × 23 + 1 × 22 + 0 × 21 + 0 × 20 + 0 × 2-1 + 1 × 2-2 + 1 × 2-3 |
| = | 12.375 (base 10) |
Conversion from binary fractions to decimal can be done in several ways. One method is, as demonstrated above, to expand the number as a sum of products of powers of two and simply evaluate the resulting expression. A table of negative powers of two can help. Alternatively, common powers of two can be factored out, as in (using 2-1 = ½)
| 0.01101 (base 2) | = | (0 + (1 + (1 + (0 + 1/2)/2)/2)/2)/2 |
| = | (0 + (1 + (1 + (0 + 0.5)/2)/2)/2)/2 | |
| = | (0 + (1 + (1 + 0.25)/2)/2)/2) | |
| = | (0 + (1 + 0.625)/2)/2 | |
| = | (0 + 0.8125)/2 | |
| = | 0.40625 (base 10) |
| 0.101111 (base 2) | = | 0.101111 × 26 × 2-6 |
| = | 101111 × 2-6 | |
| = | 47/26 | |
| = | 47/64 | |
| = | 0.734375 (base 10) |
Conversion from decimal fractions to binary is easily done by a simple iterative multiplication scheme. Assume we have a fraction, x, which we wish to express in binary. Then we wish to solve for the bits in
| x | = | X-12-1 + X-22-2 + X-32-3 + … + X-m2-m |
| 2 × x | = | X-1 + X-22-1 + X-32-2 + … + X-m2-m+1 |
| 2 × 0.435 | = 0.87 | first bit | = 0 | |
| 2 × 0.87 | = 1.74 | next bit | = 1 | |
| 2 × 0.74 | = 1.48 | = 1 | ||
| 2 × 0.48 | = 0.96 | = 0 | ||
| 2 × 0.96 | = 1.92 | = 1 | ||
| 2 × 0.92 | = 1.84 | = 1 | ||
| 2 × 0.84 | = 1.68 | = 1 | ||
| 2 × 0.68 | = 1.36 | = 1 | ||
| 2 × 0.36 | = 0.72 | = 0 | ||
| 2 × 0.72 | = 1.44 | = 1 | ||
| … | … |
| 0.435 (base 10) | = | 0.0110111101011100001010001111 |
For 0.435, for example, if we allow only two bits of precision, then we can represent only 0.00, 0.01, 0.10, and 0.11 (base 2) (0, 0.25, 0.5 and 0.75 [base 10]) and we would chose 0.10 as the closest approximation to 0.435. With 9 bits, we can represent 0.011011110 (base 2) (=0.43359375 [base 10]) and 0.011011111 (base 2) (= 0.435536875 [base 10]) but not 0.435. Obviously, as we keep increasing the number of bits used, the precision of our numbers gets better and better. In fact, if the closest binary fraction of n bits is used to represent a decimal fraction, the round-off error in representation is less than 2-n-1. With 9 bits to represent 0.435, the closest representation is 0.011011111 (base 2) (= 0.435546875 (base 10)) and the error is
| 0.435546875 - 0.435 = 0.000546875 < 0.0009765625 | = | 2 -10 |
When the position of the binary point is assumed to be in the same location for all numbers, the resulting representation is called a fixed-point number. Integers are a special case of fixed-point numbers where the binary point is assumed to be just to the right of the low-order bit. Fixed-point numbers can always be treated as if they were just integers whenever addition or subtraction is done because of the distributive law of multiplication over addition. If a and b have the binary point n bits from the right, then a × 2n and b × 2n are integers and
| a + b | = | (a + b) × 2n × 2-n |
| = | (a × 2n + b × 2n) × 2-n |
A different way to represent fractions allows the position of the binary point to vary from one number to another. This is called floating point representation. If this is done, then we need to know both the fraction and where the binary point is. So a floating point number consists of two parts, one part to give the magnitude of the number and the other to indicate the location of the binary point. Binary floating point numbers are generally thought of as equivalent to scientific notation for decimal numbers. Scientific notation, as you remember, represents a number as a fraction times a power of 10. Thus, Avogadro's number is expressed as 6.0225 × 1023, rather than as 602250000000000000000000. Planck's constant is 1.0545 × 10-27, rather than 0.0000000000000000000000000010545. Similarly, we can express numbers in binary as 0.101101 × 215 to represent 101101000000000 (base 2), and 0.111101 × 2-3 to represent 0.000111101 (base 2).
For each floating point number, we need to store only two numbers: the exponent (or characteristic) and the fraction (or mantissa). The same base can be used for all floating point numbers and need not be stored. The most popular base for floating point numbers is 2 (for obvious reasons), but some machines use 8 or 16 as the base for the exponent. The choice of exponent base is influenced by considerations of range and precision, and can in turn affect the choice of octal or hexadecimal for writing numbers.
To represent a floating point number, we have two numbers to store. Notice that both numbers can be treated as signed integers. Both numbers are commonly packed into one word for machines with large enough word sizes. For example, on the CDC 3600, a 48-bit floating point number is stored as
| sw | se | exponent | fraction |
| 2-1024 to 2+1023 | (10-307 to 10+307) |
| sf | se | exponent | fraction |
| 16-64 to 16+63 | (10-77 to 10+75) |
The number of bits allocated to the fraction determines the precision of the number. Remember that the round-off error in an n-bit fraction is less than 2-n-1 so the 36-bit fraction of the CDC 3600 means an error of less than 2-37 (about 11 decimal digits of accuracy), while the 24-bit fraction of the IBM 360/370 gives only about 6 decimal digits of accuracy. For more places of accuracy, more bits are needed to represent the fraction, and some machines use two words to represent a floating point number, with the second word being considered an extension of the fraction of the first word, as (for the IBM 360/370)
| First 32-bit word | Second 32-bit word | |||
| 1 | 1 | 6 | 24 | 32 |
| sf | se | exponent | 56-bit fraction | |
The exponents are generally stored as biased integers, using the excess 2n-1 representation, while the fraction is stored in either ones' or two's complement, or even sign and magnitude. The interpretation of a bit pattern as a floating point number can be quite complex. For example, on the CDC 3600, the exponent is stored as a biased, excess 1024 number, while the fraction is stored in ones' complement. To make things even more complex, if the fraction is negative, the entire word (including the exponent) is complemented. Thus, if the word
| 10111111101101011111111111111111111111111111111111 |
| 01000000010010100000000000000000000000000000000000 |
As another example, try
| 00111111110111100000000…00 |
There are several ways to store the number 0.111 × 2-3 as a floating point number. We could store it as 0.111 × 2-3, or 0.0111 × 2-2 or 0.000111 × 20 or 0.0000000000111 × 27. Which representation do we use? All we are doing in the alternative definitions is introducing leading zeros. Leading zeros make no contribution to the accuracy of our number; they are not significant digits. Zeros after the first nonzero digit can be significant. Thus, the trailing zeros on 0.1110000000 × 2-3 distinguish this number from 0.1110000001 × 2-3, or 0.1110000010 × 2-3. If we have only a limited number of bits to represent a floating point number, we want to store only the significant digits, not the leading zeros. This is accomplished by shifting our fraction and adjusting the exponent so that the first digit after the binary point is nonzero. This is the normalized form of a floating point number. Only zero has no one bits. It is treated as a special case with both an exponent and fraction of zero.
In general, for a base B of the exponent of a floating point number, the number is normalized if the first digit (in base B) after the radix point is nonzero. For a base 16 exponent, only the first hexadecimal digit of the fraction need be nonzero; the first bits may be zero, as in the normalized number
| 0.1A816 × 164 | = | 0.0001101010002 × 164 |
| frac × Bexp | 0 ≤ frac < 1 |
| 1/B ≤ frac < 1 |
Arithmetic with floating point numbers is more complex than with integer or fixed-point numbers. Addition consists of several steps. First, the binary points of the two numbers must be aligned. This is done by shifting the number with the smaller exponent to the right until exponents are equal. As an example, to add
| 0.111010100 × 24 | ||
| + | 0.111000111 × 22 | |
| 0.111010100 | × 24 | |
| + | 0.00111000111 | × 24 |
| 1.00100010111 | × 24 | |
An alternate policy is to round the result by adding 1 to the least significant digit if the first bit which cannot be kept is 1. This results in an addition like
| 0. | Original operands | 0.111010100 | × 24 | |
| + | 0.111000111 | × 22 | ||
| | ||||
| 1. | Align operands | 0.111010100 | × 24 | |
| + | 0.00111000111 | × 24 | ||
| | ||||
| 2. | Add | 1.00100010111 | × 24 | |
| 3. | Round result | + | 0.000000001 | |
| | ||||
| 1.00100011011 | × 24 | |||
| 4. | Normalize result | 0.100100011 | × 25 | |
Another problem for floating point numbers is overflow. Just as with integers, the addition of two large (in magnitude) numbers may produce a number which is too large to be represented in the machine. For example, if we have a 7-bit biased exponent and a 24-bit fraction, and try to add two numbers like
| 01111111110000000000000000000000 | |
| + | 01111111100000000000000000000000 |
| | |
| 1. Operands | 0.110000…00 × 263 |
| 0.100000…00 × 263 | |
| | |
| 2. Add | 1.010000…00 × 263 |
| 3. Normalize | 0.101000…00 × 264 |
A similar problem can happen when the difference between two very small numbers is being computed. For example, the difference between 0.101000000 × 2-63 and 0.101000001 × 2-63 is only 0.000000001 × 2-63, or when normalized, 0.100000000 × 2-71. If we are limited to a seven-bit biased exponent, this exponent is too large (in a negative direction) to be represented. This is exponent underflow. Normal practice for exponent underflow is to replace the result with zero, since although this is not the correct answer, it is very close to the correct answer.
The fraction of a floating point number cannot overflow, since this is corrected by adjusting the exponent, in postnormalization. Adjusting the exponent may cause exponent overflow or underflow, however.
The representation of floating point numbers is different for almost every computer. The variations which are possible include,
On many computers with a small word length, several words are used to represent a floating point number. For example, on the HP2100, a floating point number is represented by two words by
| First 16-bit word | Second 16-bit word | ||||
| 1 | 15 | 8 | 7 | 1 | |
| sf | 23-bit fraction | 7-bit exponent | se | ||
Both exponent and fraction are represented in two's complement notation. The binary point is assumed to be between the sign for the fraction and the high-order bit of the fraction.
Numbers can be represented in a computer in many ways. The basic unit of representation is the binary digit, or bit. Each number is represented by an encoding in terms of the bits of a computer word. Numbers can be represented in decimal by the binary coded decimal (BCD) scheme or in a binary positional notation. If the latter scheme is used, it is necessary to be able to convert between binary and decimal. Octal and hexadecimal schemes are sometimes used.
Since only a fixed-number of bits are allowed, overflow may occur. If subtraction is possible as well as addition, then negative numbers may result. Negative numbers can be represented in sign and magnitude, ones' complement, two's complement, or excess notation.
When multiplication and division are possible also, then fractions may need to be stored as well as integers. These can be stored as either fixed-point or floating point numbers. Floating point numbers are represented by encoding a pair of numbers representing an exponent and a fractional part in a normalized form. Exponent overflow and exponent underflow may occur as the result of operating on floating point numbers. Some numbers cannot be represented exactly as binary fractions with a given number of bits, so the precision and accuracy of the results of computation should be considered. This is influenced by the use of either truncated or rounded arithmetic.
| Binary | ||||||||||
| 1011010 | 1001000111 | 11101011 | ||||||||
| + | 0101011 | + | 110010 | + | 100100101 | |||||
| | | | ||||||||
| Octal | ||||||||||
| 567674 | 77651 | 3472010 | ||||||||
| + | 776571 | + | 1623507 | + | 7743 | |||||
| | | | ||||||||
| Hexadecimal | ||||||||||
| 143AF | F9A8C7B | 4FF58 | ||||||||
| + | 2E135 | + | 9A67B | + | 141508 | |||||
| | | | ||||||||
| Binary | Decimal | Octal | Hexadecimal |
|---|---|---|---|
| 1101 | 13 | 15 | D |
| 100110010 | |||
| 144 | |||
| 144 | |||
| 101101 | |||
| CAB | |||
| 127 | |||
| 43 | |||
| 144 | |||
| 93 | -93 | -13 | -14 | 47 | 128 | -128 | 0 | -0 |
The largest memory unit and fastest computation unit in the world would be useless if there was no way to get information into the computer or to get results back from the computer. In fact, the usefulness of many present computers is severely limited by the way in which new programs and data can be put into and results displayed from the computer. Thus, the input/output (I/O) system is an integral component of a computer system. We will see that there exist a large number of radically different devices which the computer may use for this purpose. This makes it very difficult to discuss all aspects of an I/O system. In this section, we consider first some general concepts important to an understanding of I/O, and then some specific common I/O devices.
The function of an I/O system is to allow communication between the computer system and its environment. This may mean communication with people (operators, programmers, users) and also with other machines. These other machines may be other computers (such as in a computer network), laboratory measuring devices, manufacturing equipment, switching equipment, or almost anything which can produce or receive electrical signals. Computers interact with other machines by sending electrical signals on cables. The cables are attached to the computer by interface boards which plug into slots in the computer chassis. Interface boards are flat pieces of plastic which contain the electronic circuitry to convert between the binary words of the computer and the electrical signals which go to and from the devices. Some devices are used for both input and output, while others are only input devices or output devices. For each different kind of device, a new interface board is needed.
The organization of the I/O system within the computer itself varies from machine to machine. We examine some specific organizations later. Generally, each computer manufacturer provides a collection of I/O devices which are specifically designed for use with its particular line of computers. These devices are mainly incompatible with the I/O system of other computers. However, with a suitable interface, almost any device can be attached to any computer. Thus, there is a growing number of independent vendors of I/O devices. These independent manufacturers often design their devices so that they are plug-to-plug compatible with a popular computing system (such as the IBM 360/370 system, or the PDP-11). This means that, with their interface, their I/O device looks the same to the computer as the original manufacturer's device and can be just plugged right in. (Of course, the device is faster, cheaper, or has more functions than the original manufacturer's device.)
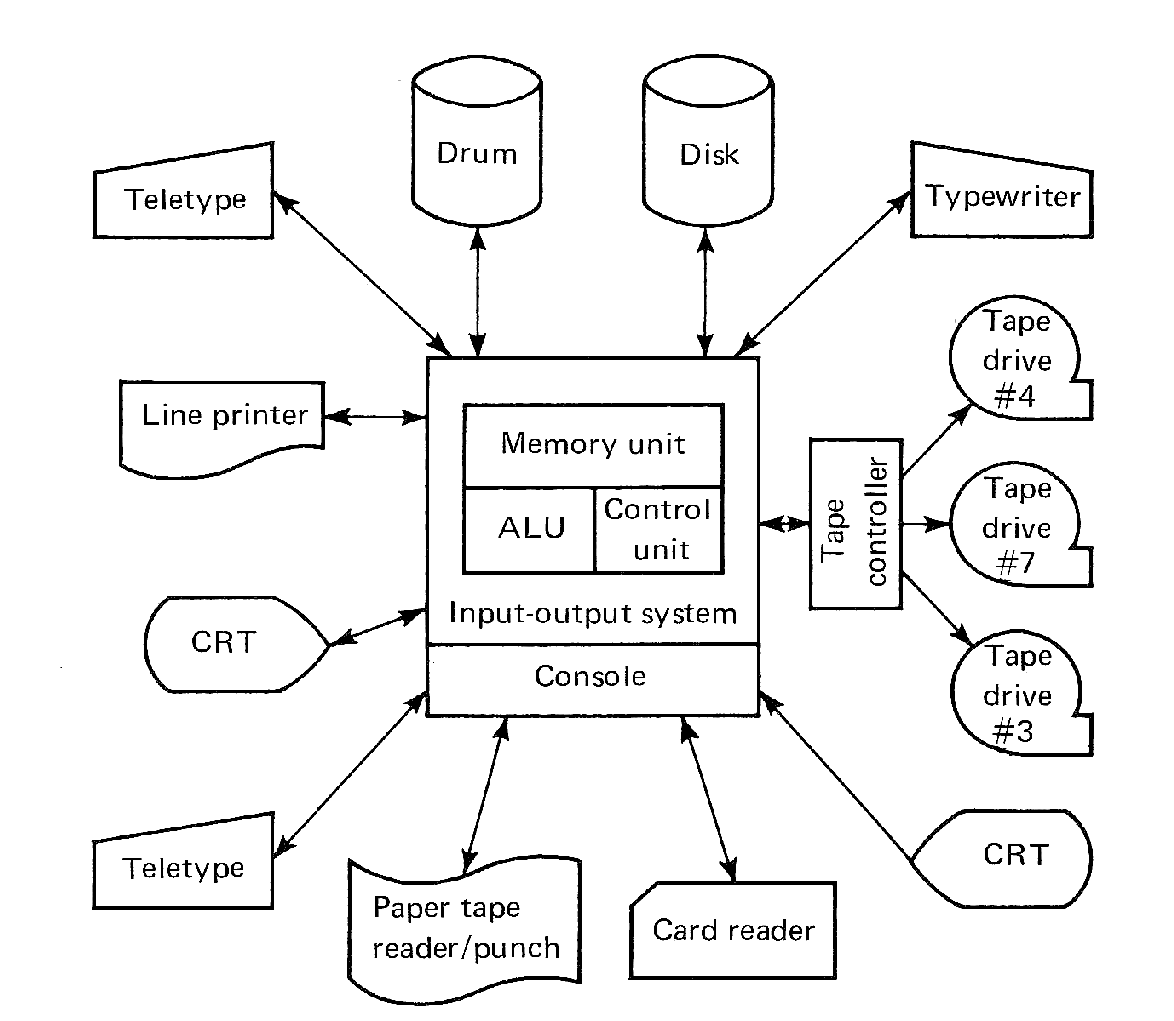FIGURE 1.6 Block diagram of computer system and peripheral devices.
Figure 1.6 illustrates a typical block diagram of a computer system which has a large number and variety of I/O devices. Since I/O devices are the interface between the machine and its users, they are called peripheral devices to distinguish them from the central computer.
In the same way that information is encoded in the memory unit (as 0s and 1s), and the computation unit (as fixed-point integers or floating point numbers), it is also encoded in the I/O system. Unlike the memory unit and computation unit, it is often not encoded in the same way for all peripheral devices. Much of the information in the I/O system is not numbers, but digits, letters, and punctuation, or characters. For instance, when a computer is handling billing information, the information is both amounts paid and owed, and the names and addresses of the people involved. These names and addresses must be represented in an encoding which the computer can store and manipulate. This is done by defining a character code. A character code is a list of the characters which can be represented and the bit pattern which is used to represent each character. Although characters can be assigned bit patterns in arbitrary ways, most computers and peripheral devices use one of three standard character codes: BCD, ASCII, or EBCDIC.
What is needed for a character code? We certainly want to be able to represent all 26 letters, 10 digits, and some special characters, such as a blank, comma, period, left and right parenthesis, plus sign, minus sign, and equals sign. A 48-character set is generally considered a minimal set, meaning that at least 6 bits must be used per character (25 = 32 < 48 < 64 = 26). The BCD (Binary Coded Decimal) character code uses 6 bits per character to define a 64-character set, including (upper case only) letters, digits, and some special characters. Table 1.6 lists a BCD character code. This is a rather than the BCD code, because there are several BCD codes, varying from machine to machine. Most of these codes agree on the representation of the letters and numbers, but many special characters will have different representations.
| Character | BCD | Character | BCD | Character | BCD | Character | BCD |
| 0 | 00 | + | 20 | - | 40 | blank | 60 |
| 1 | 01 | A | 21 | J | 41 | / | 61 |
| 2 | 02 | B | 22 | K | 42 | S | 62 |
| 3 | 03 | C | 23 | L | 43 | T | 63 |
| 4 | 04 | D | 24 | M | 44 | U | 64 |
| 5 | 05 | E | 25 | N | 45 | V | 65 |
| 6 | 06 | F | 26 | O | 46 | W | 66 |
| 7 | 07 | G | 27 | P | 47 | X | 67 |
| 8 | 10 | H | 30 | Q | 50 | Y | 70 |
| 9 | 11 | I | 31 | R | 51 | Z | 71 |
| : | 12 | < | 32 | V | 52 | ] | 72 |
| = | 13 | . | 33 | $ | 53 | , | 73 |
| ' | 14 | ) | 34 | * | 54 | ( | 74 |
| ≤ | 15 | ≥ | 35 | ↑ | 55 | → | 75 |
| % | 16 | ¬ | 36 | ↓ | 56 | ≡ | 76 |
| [ | 17 | ; | 37 | > | 57 | ∧ | 77 |
Although BCD is satisfactory for many purposes, it is too small a set of characters if upper and lower case letters and additional special characters are desired. This means at least a seven-bit code. The American Standard Code for Information Interchange (ASCII) is a seven-bit character code which allows representation of upper and lower case letters, the decimal digits, a wide variety of special symbols, and a collection of control characters for use in telecommunications. Table 1.7 gives the ASCII character code (in octal). The two- and three-letter codes (000 to 037) are control codes, mainly for use on computer typewriter-like terminals. BEL, for example, rings a bell on a teletype.
| ASCII | Character | ASCII | Character | ASCII | Character | ASCII | Character |
| 000 | NULL | 040 | blank | 100 | @ | 140 | ` |
| 001 | SOH | 041 | ! | 101 | A | 141 | a |
| 002 | STX | 042 | " | 102 | B | 142 | b |
| 003 | ETX | 043 | # | 103 | C | 143 | c |
| 004 | EOT | 044 | $ | 104 | D | 144 | d |
| 005 | ENQ | 045 | % | 105 | E | 145 | e |
| 006 | ACK | 046 | & | 106 | F | 146 | f |
| 007 | BELL | 047 | ' | 107 | G | 147 | g |
| 010 | BS | 050 | ( | 110 | H | 150 | h |
| 011 | HT | 051 | ) | 111 | I | 151 | i |
| 012 | LF | 052 | * | 112 | J | 152 | j |
| 013 | VT | 053 | + | 113 | K | 153 | k |
| 014 | FF | 054 | , | 114 | L | 154 | l |
| 015 | CR | 055 | - | 115 | M | 155 | m |
| 016 | SO | 056 | . | 116 | N | 156 | n |
| 017 | SI | 057 | / | 117 | O | 157 | o |
| 020 | DLE | 060 | 0 | 120 | P | 160 | p |
| 021 | DC1 | 061 | 1 | 121 | Q | 161 | q |
| 022 | DC2 | 062 | 2 | 122 | R | 162 | r |
| 023 | DC3 | 063 | 3 | 123 | S | 163 | s |
| 024 | DC4 | 064 | 4 | 124 | T | 164 | t |
| 025 | NACK | 065 | 5 | 125 | U | 165 | u |
| 026 | SYNC | 066 | 6 | 126 | V | 166 | v |
| 027 | ETB | 067 | 7 | 127 | W | 167 | w |
| 030 | CNCL | 070 | 8 | 130 | X | 170 | x |
| 031 | EM | 071 | 9 | 131 | Y | 171 | y |
| 032 | SS | 072 | : | 132 | Z | 172 | z |
| 033 | ESC | 073 | ; | 133 | [ | 173 | { |
| 034 | FS | 074 | < | 134 | \ | 174 | | |
| 035 | GS | 075 | = | 135 | ] | 175 | } |
| 036 | RS | 076 | > | 136 | ^ | 176 | ~ |
| 037 | US | 077 | ? | 137 | _ | 177 | DEL |
Seven bits provide for up to 128 different characters -- enough to satisfy most computer users. But 7 is an awkward number, since it is not a power or multiple of 2. Thus, many computers use an eight-bit character code. Since ASCII has an acceptable character set, the question is what to do with the extra bit. Mostly it is just left as a zero, or a one, and ignored, but for many applications it can be used to increase the reliability of the computer. For this use, the extra bit is used as a parity bit and helps to detect incorrect information.
Incorrect information can be introduced into a computer in several ways. If information is sent across wires (like telephone lines) from one location to another, static and interference can cause the information to be received incorrectly. If it is stored magnetically for a long period of time, it may change due to flaws in the magnetic medium or external magnetic fields (caused by static electricity or electrical storms, for example). Or an electronic component in the computer itself may break and cause incorrect results. In all these cases, the potential damage done by the changing of even one bit is great. For example, if the bit number 2 of the first "E" in "PETERSON" were to switch from a 1 to a 0, the "E" would change into an "A" ("E" = 1000101 ≠ 1000001 = "A"), and a Mr. Paterson might be billed, paid, credited, or shot instead of Mr. Peterson!
Parity allows this kind of error (a change of one bit) to be detected. Once the error is detected, the appropriate steps to correct the error are not immediately obvious, but that is another problem. Parity can be either even or odd. For odd parity, the extra bit is set so that the total number of 1 bits in the code for a character is an odd number. Thus, for the characters given below, the parity bit is as shown.
| Character | ASCII code | Parity | ASCII with Odd Parity |
|---|---|---|---|
| A | 1000001 | 1 | 11000001 |
| E | 1000101 | 0 | 01000101 |
| R | 1010010 | 0 | 01010010 |
| Z | 1011010 | 1 | 11011010 |
| 4 | 0110100 | 0 | 00110100 |
| , | 0101100 | 0 | 00101100 |
| (blank) | 0100000 | 1 | 10100000 |
Now suppose the same error described above happened, but the character is represented in odd parity. An "E" is represented by the bit pattern 01000101 and after bit 2 changes, the pattern is 01000001. This is no longer an "A" (11000001), and in fact, is not a legal bit pattern at all, since it has an even number of 1 bits. Since we are using odd parity, this is an error, and is called a parity error. Although we know that the character is illegal, we do not know what the original character was. It might have been an "E", but it could also have been an "I" (01001001) whose bit 3 changed, or an "A" whose parity bit changed. Also, notice that if two bits change, the parity of the result is still correct. Hence, parity bits allow us to detect some, but not all, errors. Hopefully, the more common errors will be detected.
Adding parity bits to the 7-bit ASCII code gives an 8-bit code, but only 128 characters are available. With 8 bits, up to 256 characters are possible. Although this many characters are not needed now, they undoubtedly will be someday. For this and other reasons, a third code, EBCDIC (Extended Binary Coded Decimal Interchange Code) is used by IBM for their 360/370 computers and peripherals. Table 1.8 lists some of this code. This code, as its name indicates, is similar to the BCD code.
| EBCDIC | Character | EBCDIC | Character | EBCDIC | Character | EBCDIC | Character |
|---|---|---|---|---|---|---|---|
| 00 | NULL | 40 | blank | 80 | C0 | ||
| 01 | SOH | 81 | a | C1 | A | ||
| 02 | STX | 82 | b | C2 | B | ||
| 03 | ETX | 83 | c | C3 | C | ||
| 04 | PF | 4A | ¢ | 84 | d | C4 | D |
| 05 | HT | 4B | . | 85 | e | C5 | E |
| 06 | LC | 4C | < | 86 | f | C6 | F |
| 07 | DEL | 4D | ( | 87 | g | C7 | G |
| 08 | 4E | + | 88 | h | C8 | H | |
| 09 | 4F | | | 89 | i | C9 | I | |
| 11 | DC1 | 91 | j | D1 | J | ||
| 12 | DC2 | 92 | k | D2 | K | ||
| 13 | TM | 93 | l | D3 | L | ||
| 14 | RES | 5A | 94 | m | D4 | M | |
| 15 | NL | 5B | $ | 95 | n | D5 | N |
| 16 | BS | 5C | * | 96 | o | D6 | O |
| 17 | IL | 5D | 97 | p | D7 | P | |
| 18 | CAN | 5E | ; | 98 | q | D8 | Q |
| 19 | EM | 5F | ¬ | 99 | r | D9 | R |
| 21 | SOS | A1 | s | E1 | S | ||
| 22 | FS | A2 | t | E2 | T | ||
| 23 | A3 | u | E3 | U | |||
| 24 | BYP | 6A | A4 | v | E4 | V | |
| 25 | LF | 6B | , | A5 | w | E5 | W |
| 26 | ETB | 6C | % | A6 | x | E6 | X |
| 27 | ESC | 6D | _ | A7 | y | E7 | Y |
| 28 | 6E | > | A8 | z | E8 | Z | |
| 29 | 6F | ? | A9 | E9 | |||
| 30 | B0 | F0 | 0 | ||||
| 31 | B1 | F1 | 1 | ||||
| 32 | SYN | B2 | F2 | 2 | |||
| 33 | B3 | F3 | 3 | ||||
| 34 | PN | 7A | : | B4 | F4 | 4 | |
| 35 | RS | 7B | # | B5 | F5 | 5 | |
| 36 | UC | 7C | @ | B6 | F6 | 6 | |
| 37 | EOT | 7D | ´ | B7 | F7 | 7 | |
| 38 | 7E | = | B8 | F8 | 8 | ||
| 39 | 7F | " | B9 | F9 | 9 |
Why are there different character codes? Part of the reason is historical. The original BCD code was defined to allow easy translation from the Hollerith punched card code (see Table 1.9) to the BCD code. This explains the strange grouping of 0-9, A-I, J-R, and S-Z. Special characters sort of filled in the left-over spaces. ASCII was defined with telecommunications in mind, so the letters, digits, and so forth can be put wherever convenient, trying to keep control characters, letters, digits, and so on together as much as possible to allow easy programming. EBCDIC tries to combine both of these features into its code.
What difference does it make which code is used? Within the computer, very little. Some codes are more convenient than others for some purposes. For simple English text, a BCD code requires only six bits per character rather than eight bits per character for ASCII with parity or EBCDIC; thus, only 3/4 as many bits are needed to store a given sequence of characters. We could store one character per word, but this would be intolerably wasteful of memory for large words, or long strings of characters. Hence, several characters are normally packed in each word. The number of bits needed to represent a character is called a byte. On a 24-bit machine, for example, each word has four 6-bit bytes, or three 8-bit bytes. The character code often influences the length of word (or vice versa). Hence 16-bit computers almost always use an 8-bit byte with an 8-bit ASCII code. The CDC 6600, with its 60-bit words, uses a 6-bit character code, while if its words had been 64 bits long, it probably would have used an 8-bit code. The IBM 360/370, with 32-bit words, uses the 8-bit byte with an EBCDIC code.
The character code also influences another function of the machine. It is often convenient to output lists of names in alphabetical order. It is convenient within the computer to consider each character as the unsigned integer number defined by its character code. Thus, "A" < "B" < "C" < … in all the character codes. But what about the digits, special symbols, and blanks? If the character code is used for names containing combinations of letters, digits, and special characters (like 3M, IBM 360, I/O), the alphabetical order may not be obvious, and is generally left up to the character code. Thus, on some machines "A1" is before "AA" alphabetically, while on others "A1" is after "AA". The order of the characters in the character code is called the collating sequence. If the character code in use matches our expectation for the collating sequence, then no problems arise. If not, then placing words in alphabetical order may become very complicated (or we adjust our expectations to what is easy for the computer).
The character code can also influence the ease of using various peripheral devices. A computer which is set up to use a six-bit BCD code may not be able to easily use an I/O device using ASCII or EBCDIC. Being able to use only a character set of 64 characters can limit how concepts are expressed to the computer, if these concepts are naturally expressed in terms of characters or symbols not available on the machine.
Many different I/O devices are currently in use with computer systems. Despite this wide variety, however, there are certain classes of devices which are common to many computer installations. In order to be able to understand the constraints which are placed on the computer by its peripheral devices, we consider the typical characteristics of the common I/O devices. Individual devices will differ, and specific information can be obtained only from the vendors' manuals.
Although most people do not consider the console of a computer as an input or output device, it can be a very useful means of communicating with a computer. The console generally consists of a collection of display lights, switches, and buttons. It is designed for utility and, sometimes, impressiveness. Typically, at least the following features are available on the computer console:
The console is normally designed so that an operator sitting at the console has total control over the entire computer. The display lights allow the operator to monitor the contents of all memory locations and registers. Using the switch register to give addresses and data, the operator may change the contents of selected memory locations or registers.
In the early days of computing, a programmer normally debugged programs by sitting at the console and following them through, step by step, instruction by instruction. But as computers became more expensive, this was no longer possible, and programmers had to learn to debug programs from listings and dumps of memory. The console is generally used now only by the operator. Even the operator seldom uses the console display much for most computers, using instead a console typewriter. The console typewriter is really two devices in one. An input device, the keyboard, is basically a set of typewriter keys. When the operator depresses one of the keys, the character code corresponding to that character is sent to the computer. This allows the operator to input information to a program in the computer.
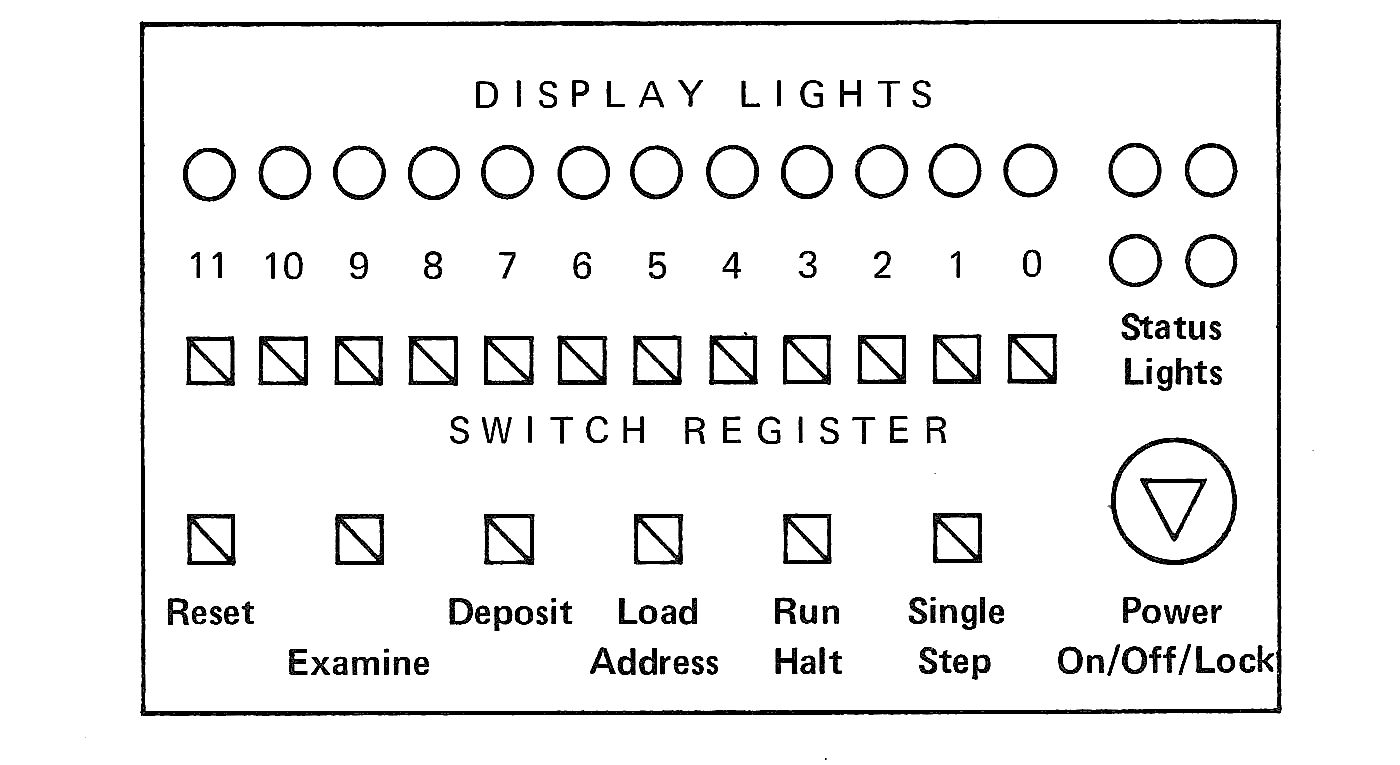FIGURE 1.7 A typical operator's console for a small computer.
The computer can send information back by outputting to the other part of the console typewriter, the printer. When a character code is sent to the printer by the computer, the printer selects the appropriate symbol and prints it on the printer paper. Normally, the operator wants the characters typed on the keyboard printed also. This can be done either by a direct link from the keyboard to the printer, or by having the computer echo print every character that is typed in.
For many early computers and some modern small computers, the console typewriter is the only I/O device available. These devices tend to be relatively slow (from 10 to 100 characters printed per second) and hence may severely limit the usefulness of the computer. Typical is the ASR-33 Teletypewriter (TTY), which operates at 10 characters per second and uses the ASCII character code. These machines are slow, mainly because of their mechanical construction, but they are also very inexpensive (about $1,000) and hence fairly popular.
One problem with using a console typewriter to input a program or data is that if an error occurs, or if it is necessary to run the program again with more data, the entire program or data must be typed again. To prevent having to type the input many times, it can be put on a machine-readable medium. One such medium is paper tape. Paper tape is normally one inch wide and slightly thicker than a normal piece of paper. It is as long as necessary. Up to eight holes can be punched across the tape. Each hole is in one of the eight channels which run along the tape. Between the third and fourth channels is the sprocket hole. The sprocket hole serves several functions. It provides a means for a mechanical paper tape reader to move the tape (like the sprocket holes on the edges of a piece of movie film). It also defines where information is on the tape. Some systems use tape with 5, 6 or 7 channels rather than 8.
Information is encoded onto the tape by punching holes in the tape. Holes correspond to 1-bits and the absences of holes to 0-bits. Normally, ASCII is used to represent the characters to be punched on the tape. Thus, each character needs seven or eight bits (depending upon whether or not parity is used). Each character is punched as a set of holes across the width of the tape, one bit per channel. For each character, a sprocket hole is also punched. The sprocket hole thus defines when a character should be looked for. Without the sprocket holes, a sequence of NULL characters with an ASCII code of 00000000 (with even parity) would be just a space of blank tape, and it would be difficult to determine how many NULL characters are on the tape.
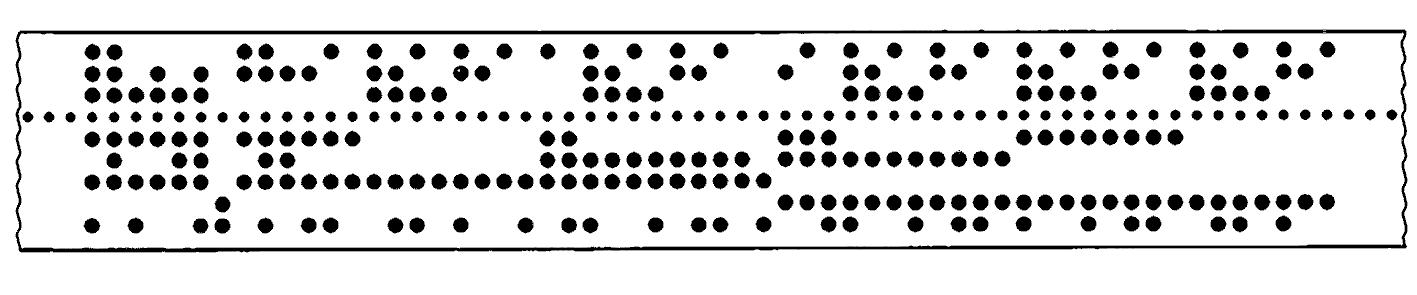FIGURE 1.8 Sample paper tape.
Paper tape is input to a computer by a paper tape reader. There are two varieties of these devices. One is electromechanical and reads the tape by using little pins which sense the presence or absence of a hole by pressing against the tape. If a hole is there, the pin moves through the tape and connects a switch; if no hole is in the tape, the pin is held back and the switch stays open. A sprocket wheel moves the tape forward one character at a time for the sensing pins. These readers operate at about 10 to 50 characters per second and are often attached to Teletypes. The ASR-33 and ASR-35 normally come with a paper tape reader attached to them, which allows input to be either from the keyboard or from paper tape.
The other paper tape readers are optical and read the tape by a set of eight photocells. The tape is moved between the photocells and a bright light. A special photocell is put under the sprocket hole to control when the other photocells are used to sense a hole or nonhole. By using a friction drive (rubber wheels, as in a tape recorder), paper tape can be read by an optical paper tape reader at speeds of up to 1000 characters per second.
Paper tape can be punched either by a special typewriter-like device (for example, a Teletype with paper tape punch attachment) which punches one eight-bit character for each key which is depressed at the keyboard, or by a computer using a paper tape punch I/O device. A computer-controlled paper tape punch can punch paper tape at a rate of about 200 characters per second.
The computer can use a paper tape punch as an output device, but, since people tend to be relatively poor at reading paper tape, it is used mainly to create output which can be easily read back into a computer at a later time. Thus, paper tape can be considered as an input medium, an output medium, and a storage medium.
One of the major problems with paper tape is the difficulty of correcting an error in the information on the tape. Programs often must be fed into the computer many times, with minor changes each time, before they are correct. Computer-punched paper tape can be wrong sometimes. Even if the tape is correct, it may become torn, or badly worn in a few spots. Generally, this requires punching a complete new paper tape.
Punched cards do not have this problem. Each card is a piece of cardboard about 3½ inches wide by 7½ inches long (the size of the dollar bill around 1900, according to computer folklore). The card is divided into 80 columns, spaced along the card. Each column has 12 rows. A small rectangular hole can be punched into any row of any column. A character can be encoded into any column by the right pattern of holes. Figure 1.9 illustrates a punched card with the letters, digits, and some special characters in a Hollerith punched card code. Both the columns and the rows are numbered: the columns from 1 to 80; the rows by 12, 11, 0, 1, 2, …, 9, from the top to bottom. A punched card code gives for each character which rows are to be punched. Table 1.9 gives one common punched card code, the Hollerith code.
FIGURE 1.9 Sample punched computer card.
Cards are prepared by using a card punch or keypunch machine. Several companies manufacture these devices, but the most common ones are the IBM model 026 and the IBM model 029 keypunches. These machines have a typewriter-like keyboard with additional keys to control the flow of cards through the machine. The keypunch operator types his or her program onto the cards, one line of the program per card. If a mistake is made, the card is simply discarded and a new one punched. In addition to punching the code representing a character in a column, the keypunch prints the character on the top of the card (above row 12), making it relatively easy for a human to read the information on a card also.
| Character | Hollerith | Character | Hollerith | Character | Hollerith | Character | Hollerith |
| blank | no punch | + | 12 | _ | 11 | ||
| 0 | 0 | A | 12-1 | J | 11-1 | / | 0-1 |
| 1 | 1 | B | 12-2 | K | 11-2 | S | 0-2 |
| 2 | 2 | C | 12-3 | L | 11-3 | T | 0-3 |
| 3 | 3 | D | 12-4 | M | 11-4 | U | 0-4 |
| 4 | 4 | E | 12-5 | N | 11-5 | V | 0-5 |
| 5 | 5 | F | 12-6 | 0 | 11-6 | W | 0-6 |
| 6 | 6 | G | 12-7 | P | 11-7 | X | 0-7 |
| 7 | 7 | H | 12-8 | Q | 11-8 | Y | 0-8 |
| 8 | 8 | I | 12-9 | R | 11-9 | Z | 0-9 |
| 9 | 9 | < | 12-2-8 | V | 11-2-8 | ] | 0-2-8 |
| : | 2-8 | . | 12-3-8 | $ | 11-3-8 | , | 0-3-8 |
| = | 3-8 | ) | 12-4-8 | * | 11-4-8 | ) | 0-4-8 |
| ' | 4-8 | ≥ | 12-5-8 | ↑ | 11-5-8 | → | 0-5-8 |
| ≤ | 5-8 | ¬ | 12-6-8 | ↓ | 11-6-8 | ≡ | 0-6-8 |
| % | 6-8 | ; | 12-7-8 | > | 11-7-8 | ^ | 0-7-8 |
Punched cards have been used for a long time, well before the invention of computers. Their first use in data processing operations was in the 1890 U.S. census. The population had been increasing so fast that data from the 1880 census took nearly eight years to process by hand, and it was projected that the processing of the 1890 census would not be finished before it was time for the 1900 census. Herman Hollerith invented the techniques used for encoding information onto punched cards and the machines to process them. He later founded a company which eventually merged with others to become the International Business Machines Corporation.
In addition to the keypunch, there are many other machines which can be used to process information punched on cards, without the help of a computer. Card sorters, duplicators, listers, verifiers, and interpreters are the more common pieces of simple card processing machines. More sophisticated machines include the collator (which can merge two card decks into one) and the tabulator, or accounting machine, which can perform simple computations to produce totals and subtotals for reports.
Because of this long history, the basic punched card code is standard for letters, digits, and certain special characters (such as "$", ".", and ","). For the more recent special characters, however, different punches are used by different computer systems. Even the codes for the IBM 026 and the IBM 029 keypunches may differ. This is one of the problems in moving a program or data from one computer to another.
Cards are read by an input device called a card reader. Each card is read, one at a time, and the information for each column is sent to the computer. Cards can be read either in an alphabetic mode, where each column is interpreted as a character according to a Hollerith code, or in column binary mode, where each column is interpreted as 12 binary digits (hole = 1, no hole = 0) and these 12 bits are sent to the computer with no interpretation as characters, digits, etc.
Cards can be read either by an optical card reader, which uses a set of photocells to detect the holes in each row, or by using a metallic brush (one brush for each row) which contacts a charged metal plate behind the card if there is a hole, or is insulated from it by the card if there is no hole. Either technique produces an electric current for a hole (1) and no current for no hole (0). Card readers can read from 200 to 1000 cards per minute or, at 80 characters per card and 60 seconds per minute, from 250 to 1300 characters per second.
Cards can be punched by hand, or if the information is already in the computer, by a computer card punch output device. A computer-controlled card punch will punch either the alphanumeric Hollerith code or column binary in a form which can be read back into a computer later, but often without the printing on the top of the card to allow a person to read it. Card punches operate at a speed of about 200 cards per minute (250 characters per second).
In addition to being able to get information into a computer by using a Teletype, paper tape, or punched cards, it is sometimes useful to be able to get information out of the computer. The printer of a Teletype can be used for this purpose, but it is normally quite slow. A card punch can be used, but this requires running the punched cards through another machine to print the information punched in them on paper, or on the cards themselves. The most common form of computer output device is the line printer. A line printer is a printer which prints, not one character at a time, but an entire line at a time. The length (or width) of a line varies from 80 to 136 characters. Each character is 1/10 inch wide, so the paper for a line printer varies from about 10 inches to 15 inches across. On each edge is a set of sprocket holes to allow the line printer to easily and accurately move the paper for each line to be printed. A page of computer paper typically has 66 to 88 lines for printing (6 or 8 lines per inch, on 11-inch paper) and each page is serrated to allow easy separation.
The line printer prints each character much the same as a typewriter would. An ink-impregnated ribbon extends along the length of the page. On one side of the ribbon is the paper; on the other, the metallic image of the character. An electrically controlled hammer (solenoid) strikes the type for the selected character, printing the character. The major difference is that where a typewriter prints one character at a time, the line printer prints all the characters at once. Sometimes they "cheat" and print first all the odd columns, then all the even columns. Some of the more inexpensive line printers separately print the first twenty characters, then the next twenty, and so forth.
The character type pieces are organized in two ways. One is as a set of type wheels (one for each character position on the line) which rotate until the correct character is opposite the paper and then print that character. With this system, it is somewhat difficult to assure that each character is positioned exactly right, so some vertical displacement sometimes occurs, which produces an output line that wiggles slightly across the page. An alternative method organizes the characters in a long circular horizontal chain which rotates at high speed along the length of the print line. When the proper character is between the hammer and the ribbon for a particular print position, the hammer fires, to print the character. This may cause some horizontal displacement, so that the character spacing is not exact, but the eye tends not to notice this. To prevent having to wait too long for a given character to appear, characters are repeated on the chain at regular intervals, so that four copies of an "A" may appear on the chain.
Normal computer paper can be used in the line printer, or special forms may be used to print checks, reports, letters, bills, books, and so on. Unlike the other devices we have seen, there is no input device which corresponds naturally with this output device. The line printer is mainly used to present the results of a computer program to users for their reading.
Nonmechanical printers are also in use. These devices employ heat or radiation to "print" on specially processed paper and can print at speeds of up to 30,000 lines per minute.
The devices and media which we have just seen are by far the most common input and output devices in use with computers today, but they are by no means the only devices. An increasingly common output device is the cathode-ray tube (CRT), commonly connected with a keyboard to replace a console typewriter or Teletype. A CRT is basically an oscilloscope or TV tube with additional electronics to allow it to interface with the computer. This device uses an electron beam to "draw" pictures on the phosphorus-coated screen, or simply to display characters. A screen can typically display 24 lines of 80 characters and imitates a Teletype by "scrolling" (a new line appears at the bottom, pushing all other lines up, and the top line disappears). CRTs are quiet, fast, and easy to use, since they are completely electronic, but they suffer from their inability to produce "hard copy" (printed copy) which can be kept for reference.
CRTs were originally connected to computers to serve as graphic output devices, for plotting functions, charts, and diagrams. Another device used for this same purpose, but capable of giving hard copy output, is the plotter. A plotter controls the movement of an ink pen over a piece of paper. The paper is either stationary on a flat surface, with the pen moving back and forth across it, or the paper moves along the surface of a cylinder, called a drum, and the pen can move left and right as the paper goes back and forth. The pen can either move in a "down" position, where the pen is touching the paper and a line is left as the pen moves, or in an "up" position, with no line being drawn. Plotters can be quite useful in displaying the results of a computation in an easily understood visual manner.
In addition to output devices, there are additional input devices. Mark sense card readers and page readers use a reflective light photocell to be able to read marks made with the standard, number 2 pencil on special mark sense forms. This eliminates the need for a keypunch, since rather than punching a hole in the form, it is only necessary to mark where the hole should be. Optical character readers are being developed which can read some types of printed characters.
IBM has introduced a 96-character punched card that is only one-third the size of a Hollerith card, but which uses 3 sets of 6 rows of 32 columns to represent up to 96 characters. Each set of 6 rows encodes a character in a 6-bit BCD code and are read in column binary mode.
Television cameras, loudspeakers, mechanical arms, toy trains, robots, and other strange devices have been attached to computers to allow communication between them and their environment, although mainly for research purposes. A large variety of devices can be attached to a computer to provide it with input and output facilities.
Very early in the use of computers, it became obvious that there simply was not enough core memory to store all the information which we wanted to process. Punching the information out on paper tape or cards was both expensive (since the medium could not be reused) and slow. A fast, relatively inexpensive means of storing large amounts of data was needed. The magnetic tape was the answer.
Magnetic tape is a long (2400 feet) reel of a flexible plastic, about ½ inch in width and coated with an iron oxide. Information is recorded by magnetizing little spots on the tape, allowing one bit of information to be recorded per spot. As with paper tape, the tape is recorded in channels, or tracks. Tapes are recorded as either seven- or nine-track tapes. This allows seven or nine bits to be recorded vertically along the width of the tape, accommodating a six- or eight-bit character code plus a parity bit. Each set of seven or nine tracks is called a frame. Along the length of the tape, information can be recorded at low density (200 bits per inch), medium density (556 bits per inch), high density (800 bits per inch) or hyper density (1600 bits per inch). The wording "bits per inch" (bpi) really means "frames per inch". Since each bit along the tape is 7 or 9 bits high, each bit along the tape can represent one character and hence, at high density, we can store 800 characters per inch of tape. If an entire tape were used to store information at 800 bpi, 23,040,000 characters could be recorded. In practice, however, it is best not to record too close to either end of the tape, and it is not practical to record information continuously on the tape.
A magnetic tape is mounted on a magnetic tape drive or tape transport to be read or written. In order to work properly, the tape must be travelling past the read-write heads of the tape drive at a fixed speed. This requires some time for the tape to "get up to speed" before reading or writing, and to stop after reading or writing. With only 1/800 inch per character, the tape drive cannot stop between characters. Thus, tape is written in blocks, or records, of information, which are read or written at one time and separated by inter-record gaps. An inter-record gap is simply a span of blank tape, typically about 3/4-inch long. The inter-record gap allows enough space for the tape drive to stop after one record and get started again before the next record. This can Considerably reduce the amount of information on a tape, however.
For example, if we copy 80 character card images to a tape, one card image per record, then at 800 bpi, a card image will take only 0.1 inch of tape. Separating each record by an inter-record gap of 0.75 inch means that less than 1/8 of the tape is being used to store information. This allows the storage of about 30,000 cards per tape.
Most tape drives have the same functions that an audio tape recorder has. They can read or write, rewind, fast forward (called skipping forward), or skip backwards. Some tape drives can also read and write tape backwards.
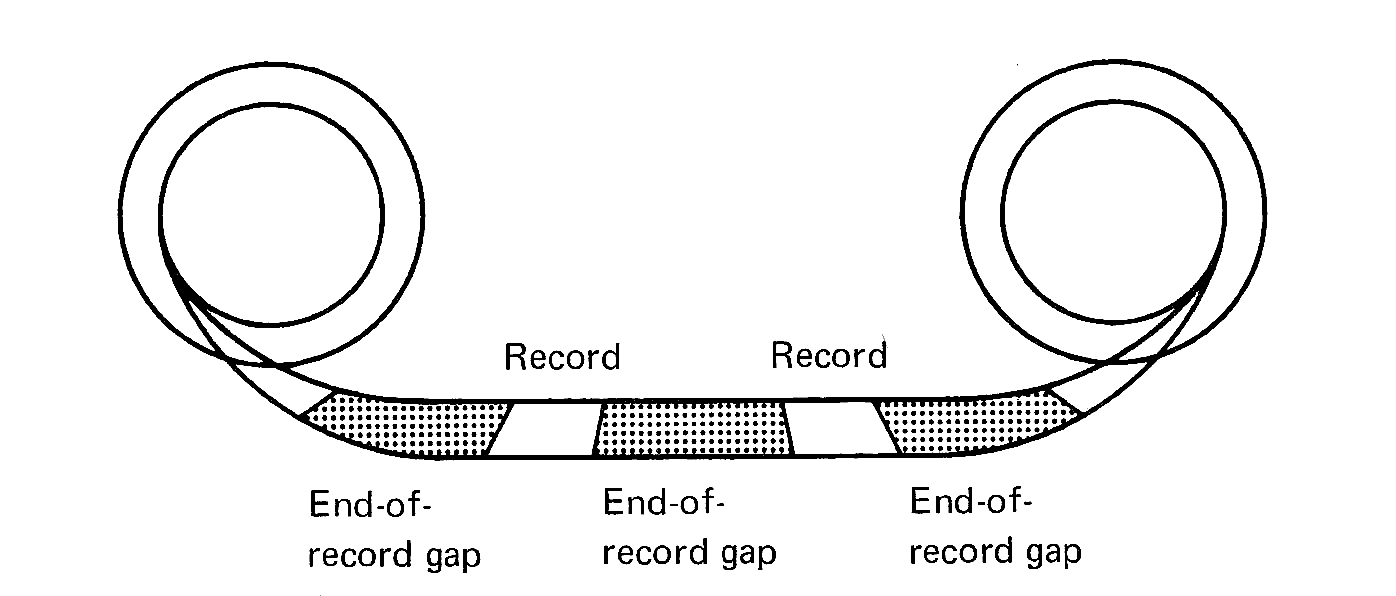FIGURE 1.10 Magnetic tape -- information is
recorded in variable-length records which are separated by inter-record gaps.
Magnetic tape can be reused; that is, written and then rewritten. One problem with normal tape drives, however, is that to write on the tape, the information which was there must be erased first. This is done automatically by an erase head that erases the tape in front of the write head, which writes the new information on the tape. The old information which was written on the tape in front of the space just written may be partially erased. Thus, magnetic tape cannot be read beyond the end of the most recent write on the tape. New or corrected information can only be added to the end of a tape. If it must be added in the middle, the entire tape must be recopied.
Another feature of magnetic tape is that the only way to determine where the information is on the tape (as opposed to just blank tape) is by having at least one 1 bit in each frame on the tape. Blank tape looks just like a character of all zeros. (This is like a paper tape with no sprocket hole.) Because of this, either odd parity must be used, or the all-zero code cannot be recorded on the tape. For the BCD code, if this code is written in even parity it is automatically converted to a 12 (octal) code, and all 12 (octal) codes are read back in as a 00 (octal) code. Thus, the character ":", which normally corresponds to a 12 (octal) code cannot be stored on a magnetic tape. In fact, there are two separate BCD codes: internal BCD, used for representing characters in memory; and external BCD, used for representing characters on tape. This is of little importance except to cause additional difficulty and confusion in the transporting of data or programs from one computer installation to another.
Tapes can be recorded in either even or odd parity. The parity bit is of great value with magnetic tapes, since the likelihood of a parity error on a magnetic tape is nonnegligible. The actual error rate per bit is quite small, but one tape can easily store a million characters, which is 7 or 9 million bits. Also, tapes are susceptible to damage from heat, dust, magnetic fields, or simple wear and tear. Whenever working with magnetic tapes, you should consider the possibility of parity errors.
Many computer systems store large amounts of data on tape and have extensive tape libraries. Hundreds or thousands of tapes may be mounted on the tape drives for use and then dismounted and put back in the library. Tapes are a removable storage media, since they can be removed from the actual tape drive and stored separately from the computer.
In addition to the large storage capacity of magnetic tapes, they can be read or written at very high speeds. It takes from 1 to 20 milliseconds to get the tape up to speed. Then 3000 to 20,000 characters per second can be transferred between the tape and core memory.
How are magnetic tapes used? Mainly, they are used as auxiliary storage devices for the computer, storing large amounts of information, either temporarily or permanently. But they are also used as input and output devices. Because of the large speed difference between card readers and line printers on the one hand and the computer on the other, the computer can spend much of its time waiting on these devices. To prevent this, these devices are sometimes run off-line. The card reader reads onto a magnetic tape, rather than directly into the computer. When the tape is full, it is taken over and mounted on a tape drive connected to the computer. The computer reads and processes the data on the input tape, producing output on an output tape. The output tape is then taken to a line printer, which is driven not by the computer but by a tape drive, and the contents of the tape is copied to the line printer. This mode of operation can be quite successful in some situations. Several manufacturers have gone one step further and provide an ability to prepare data directly on a magnetic tape by using a magnetic keyrecorder. This device is similar in operation to a keypunch, but it outputs the typed data onto a magnetic tape instead of punched cards.
One annoyance in using tapes is that they must be accessed sequentially. If we are at the rear of the tape and need some information from the front of the tape, we must rewind the tape. If we then want to continue writing, we must skip forward to the end of the recorded information to be able to write. On some problems, we must be able to store large amounts of data and be able to access it randomly and quickly. For these problems, magnetic tape is insufficient.
A magnetic disk is a form of auxiliary storage which is better than tape for these problems. A disk is very similar to a long-playing phonograph record but is made of a flat, circular metallic plate coated with ferromagnetic material. It is used in a disk drive, where it rotates at very high speeds (several thousand rpm) at all times. A read-write head is attached to an arm (like a phonograph needle) and can be positioned over any part of the disk's surface. The surface of the disk is logically divided into tracks, each track being a concentric circle. There are typically 200 tracks per disk surface, and 2 surfaces per disk (top and bottom). Several disks are attached to a spindle (like a stack of records) separated by 1 or 2 inches of space (to allow the read-write heads to move between them). All the disks rotate simultaneously, and each surface (top and bottom of each disk platter) has its own read-write head attached to a moveable arm. All the arms are ganged together and move together.
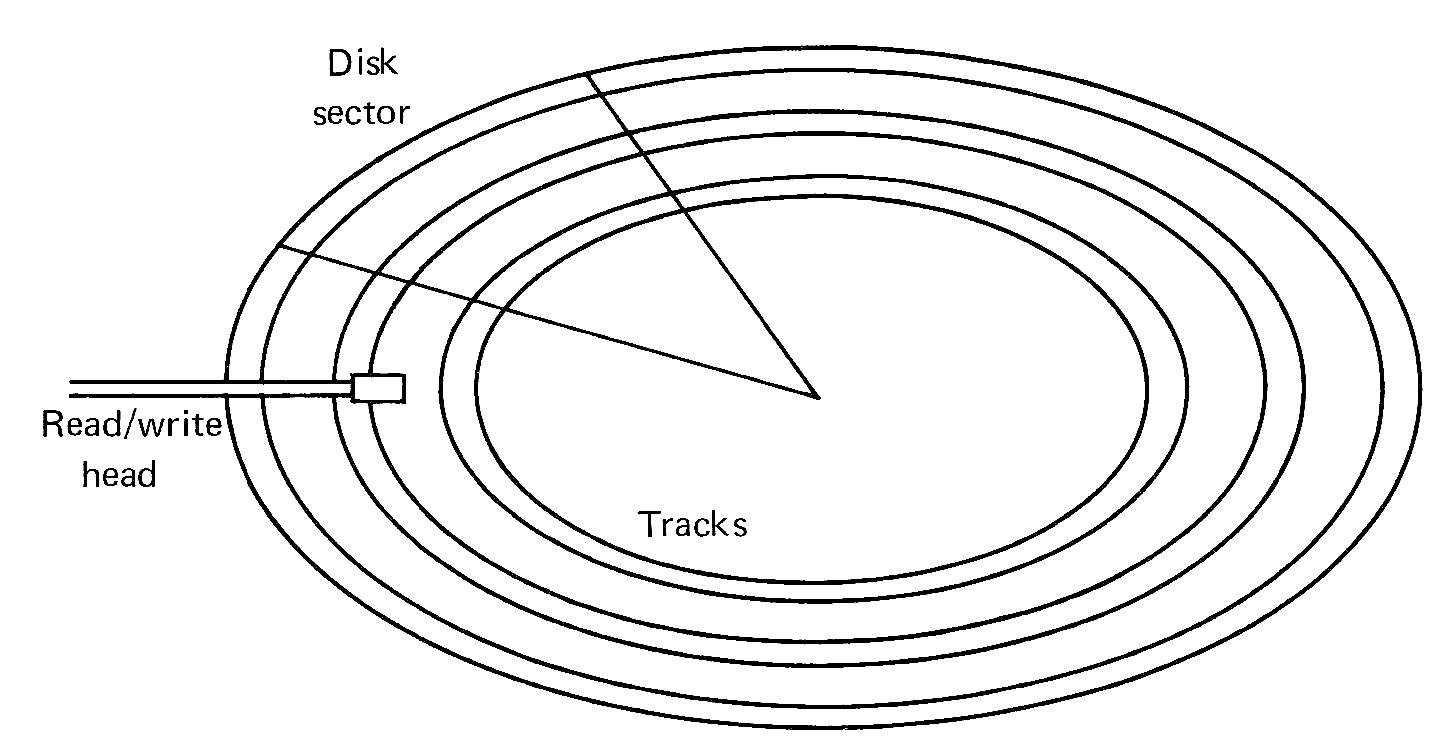FIGURE 1.11 A magnetic moving head disk. Each disk has about 200
tracks of 12 sectors per track.
In order to read or write from a specific location on the disk, the arm is moved to position the read-write heads over the correct track. When the right spot rotates under the read-write heads, the transfer of information between disk system and computer can begin. It normally takes between 20 and 600 milliseconds to position the heads depending upon how far the arm has to move and whose disk you are working with. After this seek time, there is the latency time (while waiting for the right spot to rotate under the heads), then the transfer time (while the reading or writing is done). Transfer rates for disks range from 100,000 to 1,000,000 characters per second. Disks can store up to 200 million characters, but typically store from 10 to 30 million characters. As with a phonograph record, the entire surface of the disk is not used, since we do not want too get to close to the edge or the middle.
Several variations on this basic design are used. Some disk systems have removable disk packs; that is, one set of disks can be taken off the disk drive and another mounted. This allows disk packs to be used as very high speed, large-capacity tapes. Unlike tapes, however, disks take considerably longer to get up to speed, and to slow down after use, so they are changed only infrequently. Some disk systems are designed as nonremovable devices.
If still faster access to data is needed, it is possible to eliminate the seek time by using a disk system with fixed (i.e., nonmoving) read-write heads. This requires one head for each track. One large system has 5000 separate read-write heads. With this approach, only the latency time and transfer time are important. Since read-write heads are rather expensive, a fixed head device can be very expensive. A compromise between these two extremes is to have several heads per surface -- for example, two independent movable arms, one for the inner half of the tracks on each surface, the other for the outer half of the tracks.
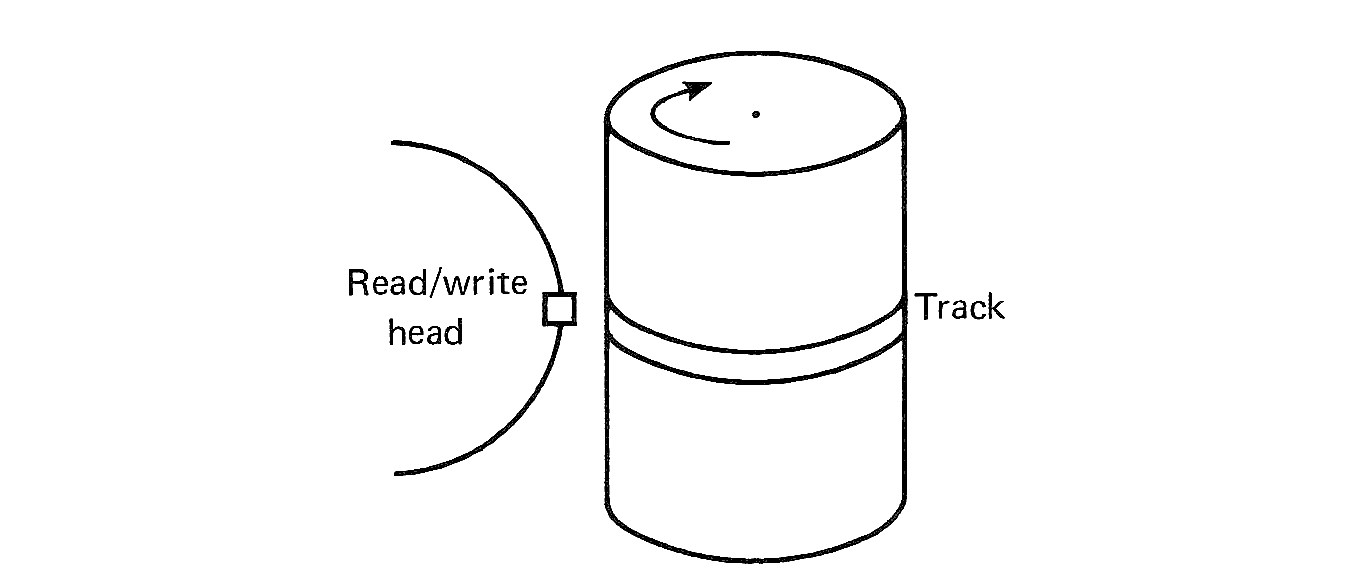FIGURE 1.12 A magnetic drum.
Similar to the design of the head-per-track disk is the magnetic drum. A drum is shaped like a cylinder and the outside surface is coated with a magnetic material. The drum rotates at high speed at all times like the disk. Similar to the disk, the recording surface of the drum is made up of tracks. Each track generally has its own read-write head. The transfer rate of a drum is usually higher than for a disk (up to 1.5 million characters per second), but the capacity is lower (from 1 to 10 million characters). Drums are nonremovable.
Just as there is a wide variety of input devices and output devices, so there is also a variety of auxiliary storage devices. Magnetic tape is being used both in the normal ½-inch magnetic tape reels and in more convenient (but smaller and slower) cassettes and cartridges. Small "floppy" disks are available that can be used very much like a flexible phonograph record. All these media are providing relatively cheap, convenient, mass storage for small computer systems.
For larger computer systems there are more exotic memory systems. Magnetic core storage is available in bulk, for use as an auxiliary storage device. Large (about a million words of memory) core memories can be built whose access times are greater than normal memory but for which sequential blocks of memory can be transferred between the bulk memory and normal memory at normal memory speeds.
Optical memories have been in use at a few computer sites for a number of years. One system used an electron beam to record on photographic film, which was then automatically developed and stored. When needed, it could be automatically retrieved and read by use of another electron beam and a photocell. Access times were on the order of seconds to minutes, but this was still faster than finding and mounting a tape. Recently, a similar system using a laser beam to burn small holes in plastic chips has been developed which provides a very large storage capacity (over a billion characters). Other new memories are being developed.
It is not possible to go into the details of all the various input/output/storage devices that are available. However, several of these devices will be referred to later in this book, and, since every computer installation will have its own devices, you should be aware both of typical devices (typewriter-like terminals, CRTs, paper tape reader/punch, card reader/punch, line printers, magnetic tapes, disks, and drums) and their general characteristics, as well as the great variety of devices a computer may use.
Each of the components of the computer system which we have discussed so far has supplied one of the necessary functions of a computer. The memory unit provides the ability to store and retrieve words quickly. The computation unit can interpret these words as numbers and perform arithmetic functions on them. The input/output system can read information into the computer or write information from the computer. But how does the memory unit know what to store, and in what location of memory? How does the computation unit know which operation to perform? How does the I/O system know when and what to transfer in or out of the computer? Obviously, the system needs some coordination between the components. This is the function of the control unit.
The control unit directs the memory unit to store information or read that information back and send it to the computation unit. It instructs the computation unit to perform a specific operation and what to do with the result (send it back to memory or to a register). The control unit directs the I/O system to transfer information and tells it where the information is and where it should go. The control unit supervises the operation of the entire computer system.
How does the control unit know what to do? In some special purpose computers, the control unit is built to perform one specific task and is designed to do this and only this. For general purpose computers, the specification of what the control unit is to do is supplied by a program. A program is a sequence of instructions to the computer which the control unit uses to control the operation of the memory unit, the computation unit, and the I/O system. The control unit executes continuously the following instruction execution cycle:
Instructions are stored as words in memory, in the same way that data is stored. In order to locate the word in memory which is the next instruction to be executed, the address of the memory location which is storing that instruction is needed. This address is stored in a register in the control unit, called the program counter or instruction address register. The name of this register varies from computer to computer. In order to fetch the next instruction to be executed, this address is sent to the memory unit by copying it into the memory address register. The memory unit is then ordered to read, and when the read portion of the read-write cycle is over, the result has appeared in the memory data register. This is copied back to the control unit and put into an instruction register. The instruction address register is then incremented to the address of the next location in memory. Under normal circumstances, this will be the address of the next instruction to be fetched.
There are many different instructions that most computers can execute. The set of instructions which a computer can execute is called its instruction set, or instruction repertoire. Each computer tends to have its own instruction set, although many computers have similar or compatible repertoires. Since instructions are stored in memory, they must be encoded into a binary representation. As with all the other encodings of information, the decision as to how the encoding is done is strictly arbitrary; it can be done in many different ways. Some ways make the subsequent construction of the control unit easier, others make it more difficult. We consider now some of the general systematic methods used to encode instructions, but this general review does not cover all the many different ways instructions are represented.
One of the first problems is to decide what is an instruction. One approach is to consider every operation which differs from another in any way to be a different, unique, instruction. Thus, storing a zero word in location 21 of the memory is a different instruction from storing a zero word in location 47. More commonly, these are considered to be the same instruction, with the address of the location to be set to zero treated as an operand. Some instructions may have several operands. For example, an "add" instruction may have three operands: the location of the augend, the location of the addend, and the location in which the sum is to be put. Thus, a specific instruction is made up of an operation and a number (perhaps zero) of operands. The operations are assigned operation codes (opcodes), which are generally binary numbers. The operands are specified by the address of a location in memory, an integer number, or a register name.
The different components of an instruction are specified by different portions of the computer word which specifies a particular instruction. A word is composed of fields, one field specifying the opcode, and the others specifying modifications of the operation, or operands of the instruction. The instruction format defines where each field is in a word, how large it is, and what it is used for. For example, on the HP2100, the instruction format is
| D/I | opcode | Z/C | operand address |
| 0010110010101110 |
The number of bits which are available for the opcode field determines the number of different instructions which can be in a computer instruction set. Thus, the HP2100 can have up to 16 different instructions because it has a 4-bit opcode field.
Some machines have different instruction formats for different opcodes. For example, on the IBM 7090, five different instruction formats were used, with the decision between different formats made on the basis of the opcode. This allows different operations to have a varying number and kind of operands. For example, an instruction which halts the computer need have no operand, while an instruction which stores a zero in a memory location needs one operand, which is the address of the memory location, and an add instruction like the one described above may need three operands. In addition to being of different formats, instructions may also be of different lengths, with some instructions occupying two or three words of memory, rather than just one.
When a computer is being designed, the specification of the instruction set is one of the major problems that must be considered. The desire to have a large set of instructions must be balanced against the difficulty of building the control hardware to execute those instructions. The instruction set is sometimes tailored to be able to efficiently solve specific kinds of problems. On the IBM 360, for example, two different, but similar, instruction sets -- the business instruction set and the scientific instruction set -- were developed. Most of the instructions were the same in both sets, but some additional instructions for character handling and decimal arithmetic were included in the business set, while floating point operations were added to the scientific set. The instruction set is one of the major differences between computers.
On the other hand, although specific instructions vary from computer to computer, almost every computer has similar instructions. Instructions can be grouped into classes of similar instructions. Typical classes are
These classes of instructions are by no means well-defined or complete. Some instructions may belong to several classes (like the instruction which tests the status of an I/O device and is hence both an I/O instruction and a Test instruction). The classes could also be further refined into more specific sets of instructions, but this could result in a very large number of classes. These classes should give you an idea of the types of instructions which are typical.
For all computers, the basic instruction execution cycle is the same. With the additional information about instructions we have now gained, we can give a better statement of the instruction execution cycle which the control unit follows:
So far we have been considering general principles that apply to all computers. As we have seen, there are many decisions which need to be made in the design of a computer. The basic parts of a computer are the memory unit, the computation unit, the input/output system, and the control unit, but in any given computer these units will be designed and built in a specific way. The specific design of both the components of a computer and their interconnections defines the architecture of the computer. The architecture of a computer defines what registers are used and for what, what the pathways in the computer are for, data and instruction formats, and how the basic units are connected.
Most books for a course on assembly language programming have introductory chapters discussing the general structure of computers. Ullman (1976) and Gear (1974) are such books. More complete and detailed information is contained in Sloan (1976), Tanenbaum (1976), and Stone (1975). These books are concerned solely with the organization and architecture of computer systems.
In order to learn how the architecture affects the ways computers are used, what computers can do, and how they do it, a specific computer design, the MIX computer, is examined (Chapters 2 and 3). After the background information necessary for a good understanding of this particular computer is presented, some other computer designs are presented (Chapter 10) to illustrate how these systems are different from and similar to the MIX computer.