| Home | Up | Questions? |
In Chapter 4 we presented a number of problems which have been defined for Petri nets. These problems concern various properties of Petri net structure and behavior which, under appropriate circumstances, would be of interest to users of Petri nets.
Two solution techniques were also presented: the
reachability tree and matrix equation approaches. These two
techniques allow properties of safeness, boundedness,
conservation, and coverability to be determined for Petri
nets. Also, a necessary condition for reachability was
established. However, these analysis techniques are not
sufficient to solve several other problems, especially
liveness, reachability, and equivalence. In this chapter we
explore these problems, either to find solutions to them or
at least to learn more about the properties of Petri nets.
5.1. Reducibility Between Analysis Problems
A fundamental concept which we use is reducibility [Karp 1972]. Solving a problem involves reducing it to another problem which we already know how to solve. For example, in the previous chapter, the problem of determining if a Petri net is conservative was reduced to solving a set of simultaneous linear equations. The problem of solving sets of simultaneous linear equations has in turn been reduced to a defined sequence of arithmetic operations (addition, subtraction, multiplication, division, and comparisons). Thus, since the simpler arithmetic operations can be computed, conservation can be determined.
Another example concerns the equality problem and subset problem for reachability sets.
Two other considerations are of importance when considering analysis problems and reducibility. First, in trying to find a solution, we must consider the possibility that a problem has no solution technique; it is undecidable. Second, if a solution technique exists, we need to consider its cost: How much time and memory space are needed? For Petri nets to gain widespread general use, analysis problems must be solvable and by algorithms which are not excessively expensive in computer time or space.
Reducibility plays a role in both of these problems. Reducibility between problems is commonly used to show that a problem is decidable or undecidable. Our approach to decidability theory [Davis 1958; Minsky 1967] is based mainly on the work of Turing and on his model of computations, the Turing machine. The importance of the Turing machine is that it is a reasonable representation of a limited computing machine and that it can be shown that no algorithm exists which can solve certain Turing machine problems, especially the halting problem. From this basis, a collection of undecidable problems has been found. The importance of this theory is that it is not possible to produce a computer program which solves these problems. Thus, for practical analysis, these undecidable problems must be avoided, or the analysis questions will be unanswerable.
(An important distinction here is that undecidable problems produce questions which are not simply unanswered but unanswerable. Questions can be unanswered but still answerable; this merely means that no one has yet found an answer but that the answer does exist. A famous example is Fermat's last theorem: Does the equation xn + yn = zn have solutions for n > 2 and nontrivial integer x, y, and z? This question has not been answered, but it is answerable. The answer is either yes or no. One way to answer the question is to produce numbers x, y, z, and n which satisfy the theorem. The other way would be to prove (logically deduce) that no such x, y, z, and n can exist. No one has yet done so.
However, assume that the problem were undecidable. Then it is not possible to decide whether x, y, z, and n exist which solve the equation. This means we could not logically deduce their nonexistence from the axioms of mathematics and that we cannot produce x, y, z, and n which solve the equation. But if we cannot produce x, y, z, and n, then they must not exist. If they did exist, we could set a computer to searching for them, and, eventually, it would find them. But if x, y, z, and n do not exist, then the answer to the question is no, and we have decided it. This contradicts our assumption that the question is undecidable, so the question is decidable.)
Now assume that a problem A is reducible to a problem B: An instance of problem A can be transformed into an instance of problem B. If problem B is decidable, then problem A is decidable, and the algorithm for problem B can be used to solve problem A. An instance of problem A can be solved by transforming it to an instance of problem B and applying the algorithm for problem B to determine the solution. Thus, if problem A is reducible to problem B and problem B is decidable, then problem A is decidable.
The contrapositive is also true: If problem A is reducible to problem B and problem A is undecidable, then problem B is undecidable; for if problem B were decidable, the above procedure is a decision technique for problem A, contradicting its undecidability. These two facts are central to most decidability techniques. To show that a problem is decidable, reduce it to a problem which is known to be decidable; to show that a problem is undecidable, reduce a problem which is known to be undecidable to it.
We shall make good use of this approach to reduce the amount of work we must do. For example, since the equality problem for reachability sets is reducible to the subset problem, we want to develop either (1) a solution procedure for the subset problem or (2) a proof that the equality problem is undecidable. If we can show (1), we have a solution technique for both problems; if we show (2), we know both problems are undecidable.
In some cases, we may be able to do even better. Two problems are equivalent if they are mutually reducible. That is, problem A is equivalent to problem B if problem A is reducible to problem B, and problem B is reducible to problem A. In this case, either both problems are decidable or both are undecidable, and we can work on either one. (Notice that this is not true in general. For example, if we were to show that the subset problem for reachability sets is undecidable, this would tell us nothing about the decidability or undecidability of the equality problem.)
The second consideration for investigating analysis problems is that if a solution technique exists it must be reasonably efficient. This requires that the amount of time and memory space needed by an algorithm to solve an instance of the problem not be excessive. The study of the cost of executing an algorithm is a part of complexity theory. Complexity theory deals with the amount of time and space needed to solve a problem. Obviously the amount of time and space will not be constant but will vary with the size of the problem to be solved. For Petri nets, time and space requirements would probably be a function of the number of places and transitions. Other factors which might influence things would be the number of tokens in the initial marking or the number of inputs and outputs for each transition and place (the number of arcs in the graph).
The time and space needed will vary with the particular instance of the problem to be solved. Therefore, complexity results may be in the form of a best case (lower bound) or worst case (upper bound) for an algorithm. Since it is not known in advance whether an instance will be a best case or worst case, the worst case is generally assumed, and the complexity of an algorithm is the worst case time or space requirements, as a function of the size of the input.
Complexity analysis is mainly concerned with the underlying problem complexity, and not concerned with a specific detailed implementation of any particular algorithm. Thus, complexity theory ignores constant factors. Complexity for a problem of size n is determined to be of order n2 or en or n log n allowing for smaller terms and constant factors. In particular two general classes of algorithms are important: those with polynomial complexity ( n, n2, n log n, n8, and so on) and those with nonpolynomial complexity (especially exponential, 2n, and factorial, n ! ).
Complexity analysis is generally applied to specific algorithms but can also be applied to general problems. In this case, a lower bound on the complexity of all algorithms to solve a problem is determined. This provides an algorithm-independent complexity result. It also can be useful in showing that a particular algorithm is optimal (within a constant) and when further work may produce a significantly better algorithm to solve a problem. For example, it is well-known that sorting n numbers is of complexity n log n. Thus algorithms with n log n complexity cannot be significantly improved on (in the asymptotic worst case).
Reducibility can be useful in determining complexity. If a problem A can be reduced to a problem B and B has a complexity fB ( n ), then the complexity of A is at most the complexity of B plus the cost of the transformation from A to B (keeping in mind that the size of the problem may also change in the transformation). The complexity of the transformations is generally constant or linear and so is often ignored. Thus, reducing problem A to problem B gives either an upper bound for the complexity of A (if the complexity of B is known) or a lower bound for the complexity of B (if the complexity of A is known). Again by using as an example the equality and subset problems, the amount of work needed to solve the equality problem is no greater than twice the amount of work for the subset problem. Since this is a constant factor, the complexity of the subset problem should be the same as the complexity of the equality problem.
These two properties of Petri net analysis properties --
decidability and complexity -- are of major concern for the
use of Petri nets. In this chapter we present some results
which have been obtained. One of the techniques used is to
reduce one Petri net problem to another.
5.2. Reachability Problems
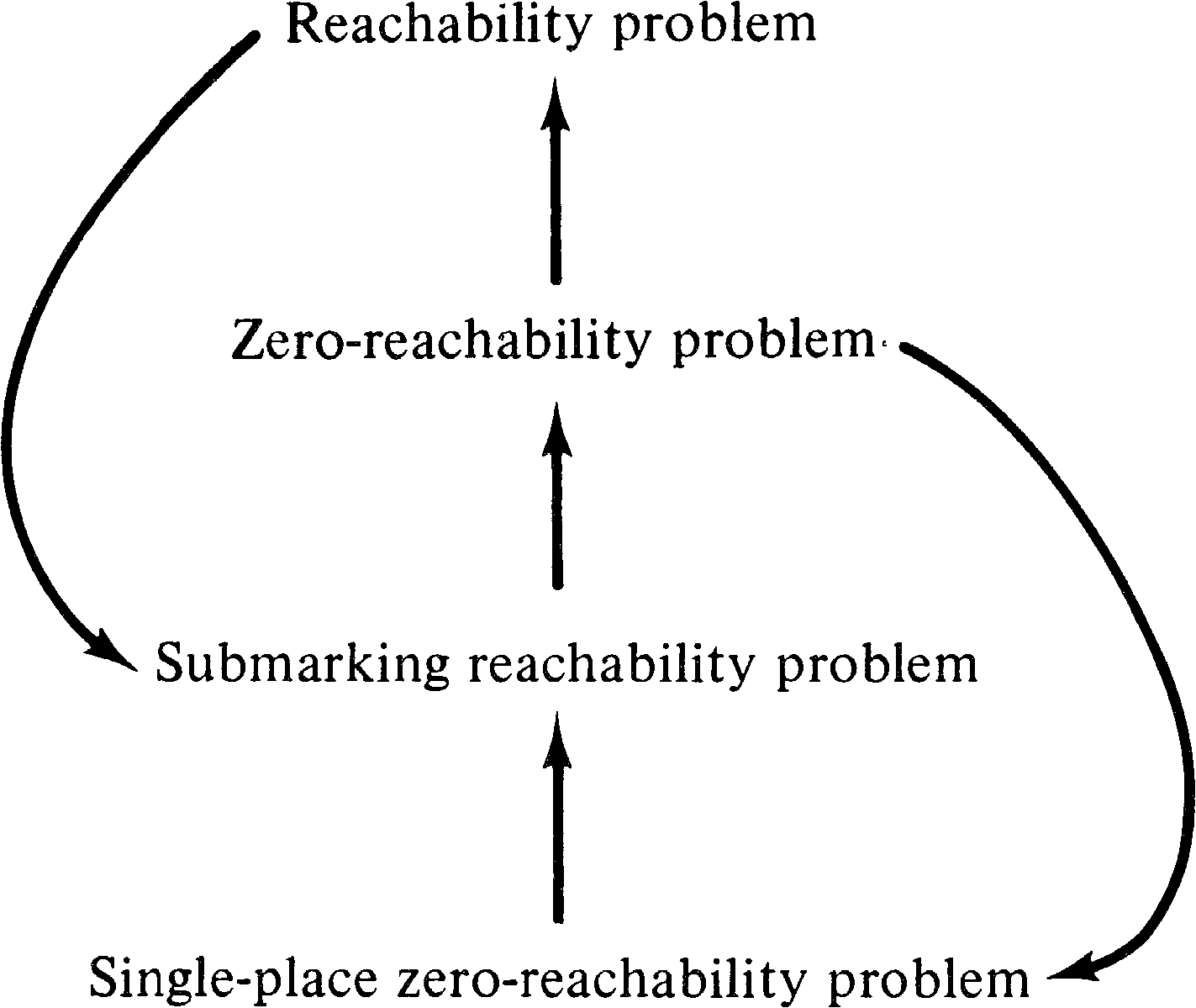
The reachability problem is one of the most important problems for Petri net analysis. It is also open to a large amount of variation in definition. The following four reachability problems for a Petri net C = (P, T, I, O) with initial marking μ have been posed.
Although these four problems are all different, they are all
equivalent. Certain relationships are immediately obvious.
The zero-reachability problem is reducible to the
reachability problem; we simply set μ′ = 0 for the
reachability problem. Similarly the reachability problem is
reducible to the submarking reachability problem, by setting
the subset P′ = P. The single-place zero-reachability
problem is reducible to the submarking reachability problem
by setting P′ = { pi } and
μ′ = 0 . More difficult to show is that the submarking
reachability problem is reducible to the zero-reachability
problem and that the zero-reachability problem is reducible
to the single-place zero-reachability problem. This entire
set of relationships is shown in Figure 5.1.

First, we show that the submarking reachability problem is reducible to the zero-reachability problem. Assume we are given a Petri net C1 = (P1, T1, I1, O1 ) with initial marking μ1, a subset of places P′ ⊆ P1, and a marking μ′ . We want to know if there exists μ′′ ∈ R ( C1, μ1 ) with μ′ ( pi ) = μ′′ ( pi ) for all pi ∈ P′ . Our approach is to create a new Petri net C2 = (P2, T2, I2, O2 ) with initial marking μ2 such that there exists μ′′ ∈ R ( C1, μ1 ) with μ′ ( pi ) = μ′′ ( pi ) for all pi ∈ P′ if and only if 0 ∈ R ( C2, μ2 ) .
The construction of C2 from C1 is quite straightforward. We start with C2 the same as C1. To allow any place pi not in P′ to become empty we add a transition ti′ with input { pi } and null output. This transition can fire whenever there is a token in pi to drain off any tokens which may reside here. This allows us to ignore these places, being sure that they can always reach a zero marking.
For places pi in P′, we must assure
that exactly μ′ ( pi ) tokens are in
pi. To assure this we create a new place
pi′ for each pi ∈ P′
with an initial marking of
μ′ ( pi ) tokens and a transition
ti′ with input
{ pi, pi′ } and null output.
If there are exactly μ′ ( pi ) tokens in
pi, then this transition can fire exactly
μ′ ( pi ) times, reducing the markings
of pi and pi′ to zero.
If the number of tokens in pi is not
μ′ ( pi ), then the transition
ti′ can only fire the minimum of the
two markings, and so tokens will be left in either
pi or pi′, preventing
the zero marking from being reached.
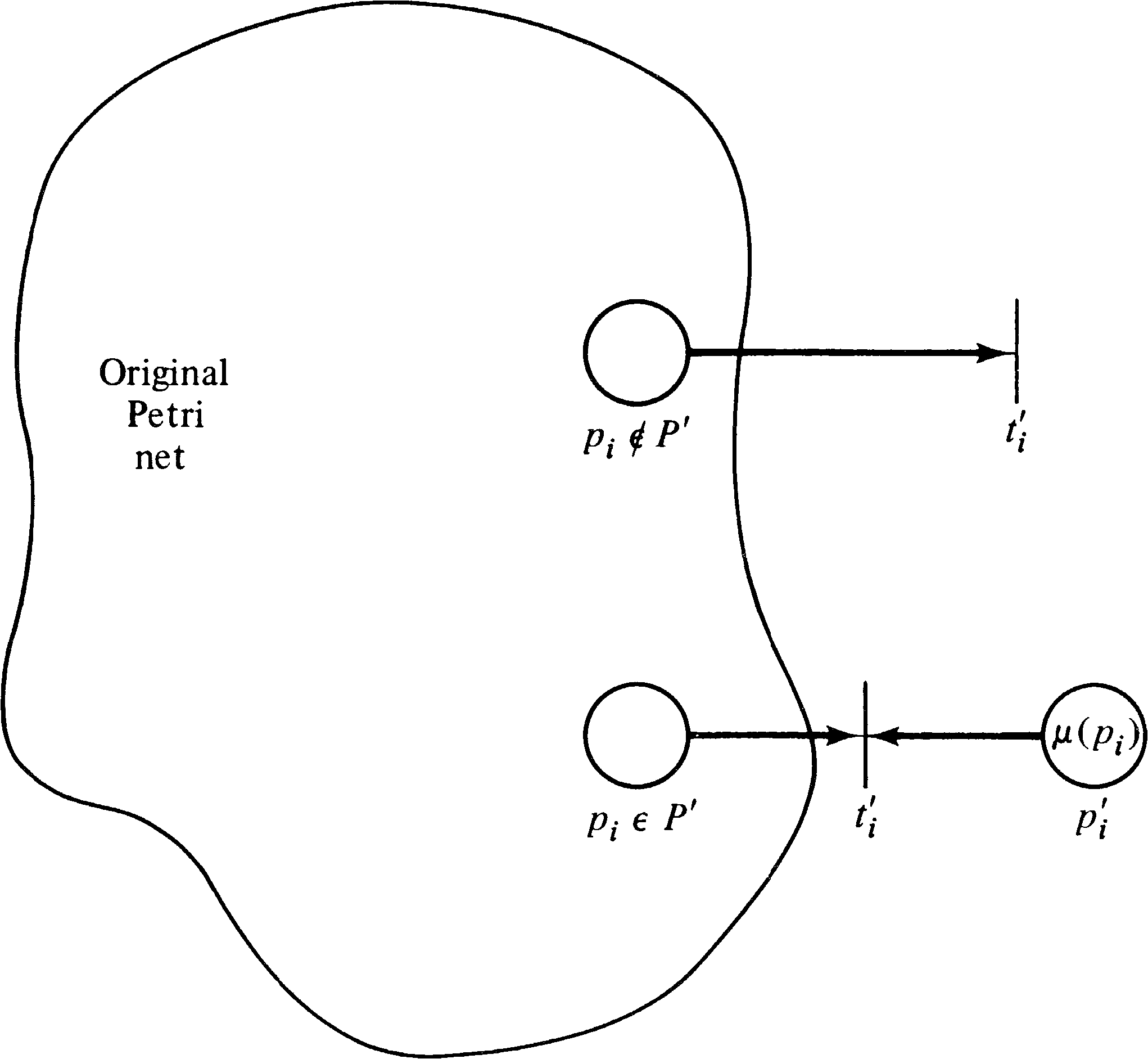
Figure 5.2 illustrates the two types of transitions
introduced. Formally we define C2 by
| P2 | = | P1 ∪ { pi′ | pi ∈ P′ } |
| T2 | = | T1 ∪ { ti′ | pi ∈ P1 } |
| I2(tj) | = | I1(tj) for tj ∈ T1 |
| I2(ti′) | = | { pi } for pi \o′/∈′ P′ |
| = | { pi, pi′ } for pi ∈ P′ | |
| O2(tj) | = | O1(tj) for tj ∈ T1 |
| O2(ti′) | = | { } for pi ∈ P1 |
| μ2(pi) | = | μ1(pi), pi ∈ P1 |
| μ2(pi′) | = | μ′(pi), pi ∈ P′ |
To show that 0 ∈ R ( C2, μ2 ) if and only if there exists a μ′′ ∈ R ( C1, μ1 ) with μ′′ ( pi ) = μ′ ( pi ) for pi ∈ P′, assume first that μ′′ exists in R ( C1, μ1 ) . Then in C2 we can also reach the marking μ′′ in the places pi ∈ P1 by firing only those transitions from T1. Now for each pi ∈ P′, we can fire ti′ exactly μ′ ( pi ) times, reducing both pi and pi′ to zero. Then we can fire ti′ for each pi ∉ P′ as many times as necessary to put these to zero, so 0 ∈ R ( C2, μ2 ) .
Now assume 0 ∈ R ( C2, μ2 ) ; then there
exists a sequence of transition firings σ which
leads from μ2 to 0. This sequence will contain
exactly μ′ ( pi ) firings of
ti′ for
pi ∈ P′ (to remove the tokens from
pi′ ) and some number of firings of
ti′ for
pi ∉ P′ .
Note that these transition firings
only remove tokens from C1, and since
δ ( μ′, tj ) is defined whenever
δ ( μ, tj ) is defined for
μ′ ≥ μ (extra tokens never hurt), the
sequence σ with all ti′ firings
removed is also legal and will lead to a marking
μ′′ with exactly
μ′ ( pi ) tokens in pi
for pi ∈ P′ . Thus if 0 ∈ R ( C2, μ2 ), then
μ′′ ∈ R ( C1, μ1 ) with
μ′′ ( pi ) = μ′ ( pi )
for pi ∈ P′ .
Q.E.D.
Our next task is to show that the zero-reachability problem is reducible to the single-place zero-reachability problem. The proof of this statement again involves a construction. Given a Petri net C1 = (P1, T1, I1, O1 ) with initial marking μ1, we wish to determine if 0 ∈ R ( C1, μ1 ) . We construct, from C1, a new Petri net C2 with an additional place s (P2 = P1 ∪ { s } ) such that there exists a marking μ′ ∈ R ( C2, μ2 ) with μ′ ( s ) = 0 if and only if 0 ∈ R ( C1, μ1 ) .
The construction of C2 defines s so that at all
times the number of tokens in s is equal to the sum of
the number of tokens in the places of C1. Thus if
μ′ ( s ) = 0, then there are zero tokens in all
places of C1 and vice versa. We define the initial
marking μ2 by
| μ2(pi) | = | μ1(pi) for pi ∈ P1 | |
| μ2(s) | = | Σ | μ′(pi) |
| pi ∈ P1 | |||
| dj | = | Σ | #(pi, O(tj)) − #(pi, I(tj)) |
| pi ∈ P1 |
The early work on Petri nets, and some current work, defined Petri nets in somewhat more restricted ways than the definition in Chapter 2. In particular, the following two restrictions are sometimes enforced.
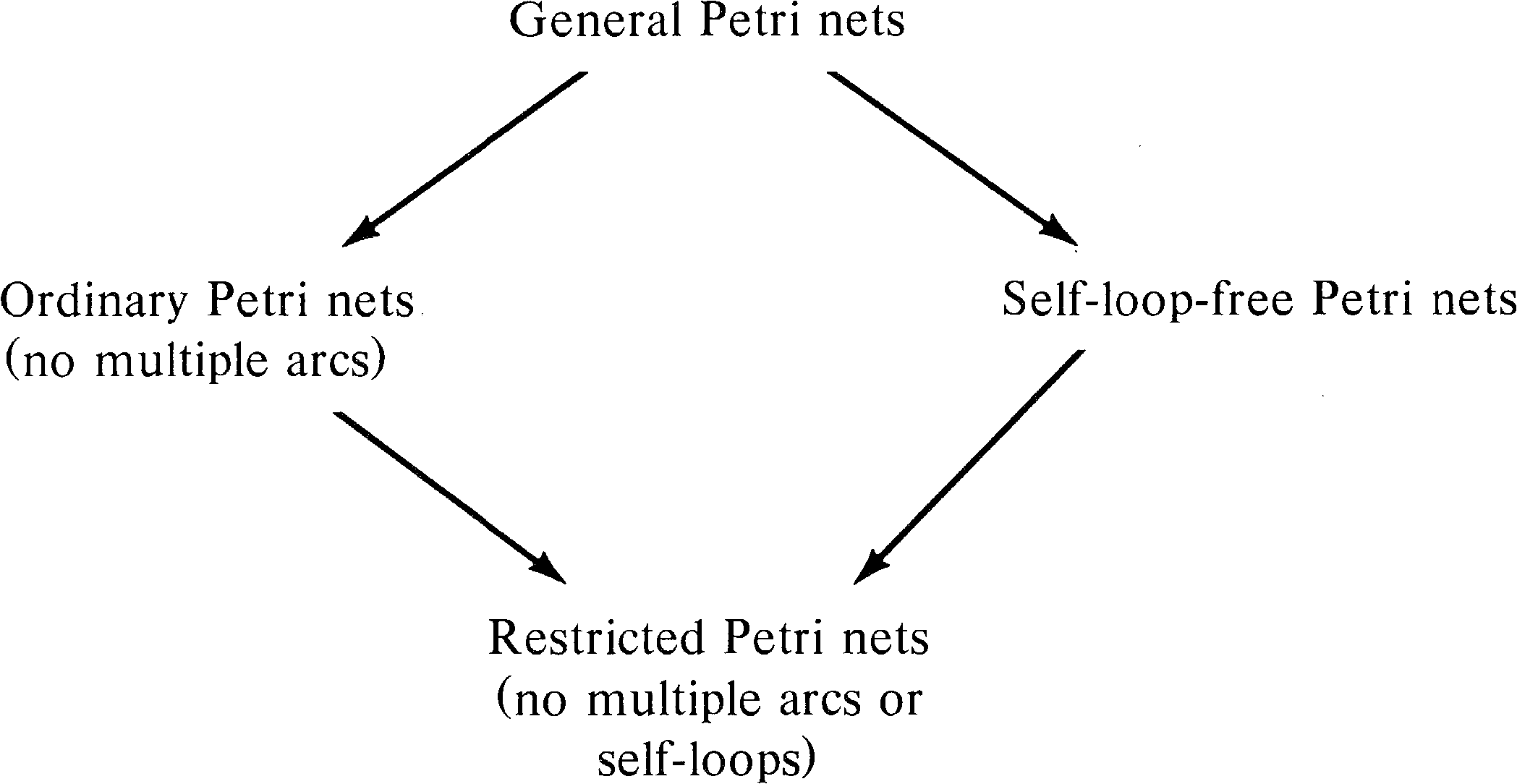
These subclasses of the general Petri net model have been considered for several reasons. A major reason is that the propagation of Petri net concepts was informal in its earlier theory. The need for multiple arcs or self-loops did not occur in early modeling. Also, it was probably felt that the theory would be easier without these additional complications to the theory. As the theory has developed, however, it has become evident that the more general definitions have not been more difficult to work with. Current work using models with these restrictions is thus either the result of unnecessary timidity on the part of the researcher or the need for quicker exposition leading to simpler definitions.
However, these restrictions add nothing to our ability to analyze Petri nets. Consider the reachability problem for these classes of nets. To show the essential equivalence of these four classes of Petri nets, we prove the following.
We show that general Petri nets can be transformed into restricted Petri nets in such a way as to reduce the reachability problem for general Petri nets to the reachability problem for restricted Petri nets. This then shows that these four reachability problems are equivalent.
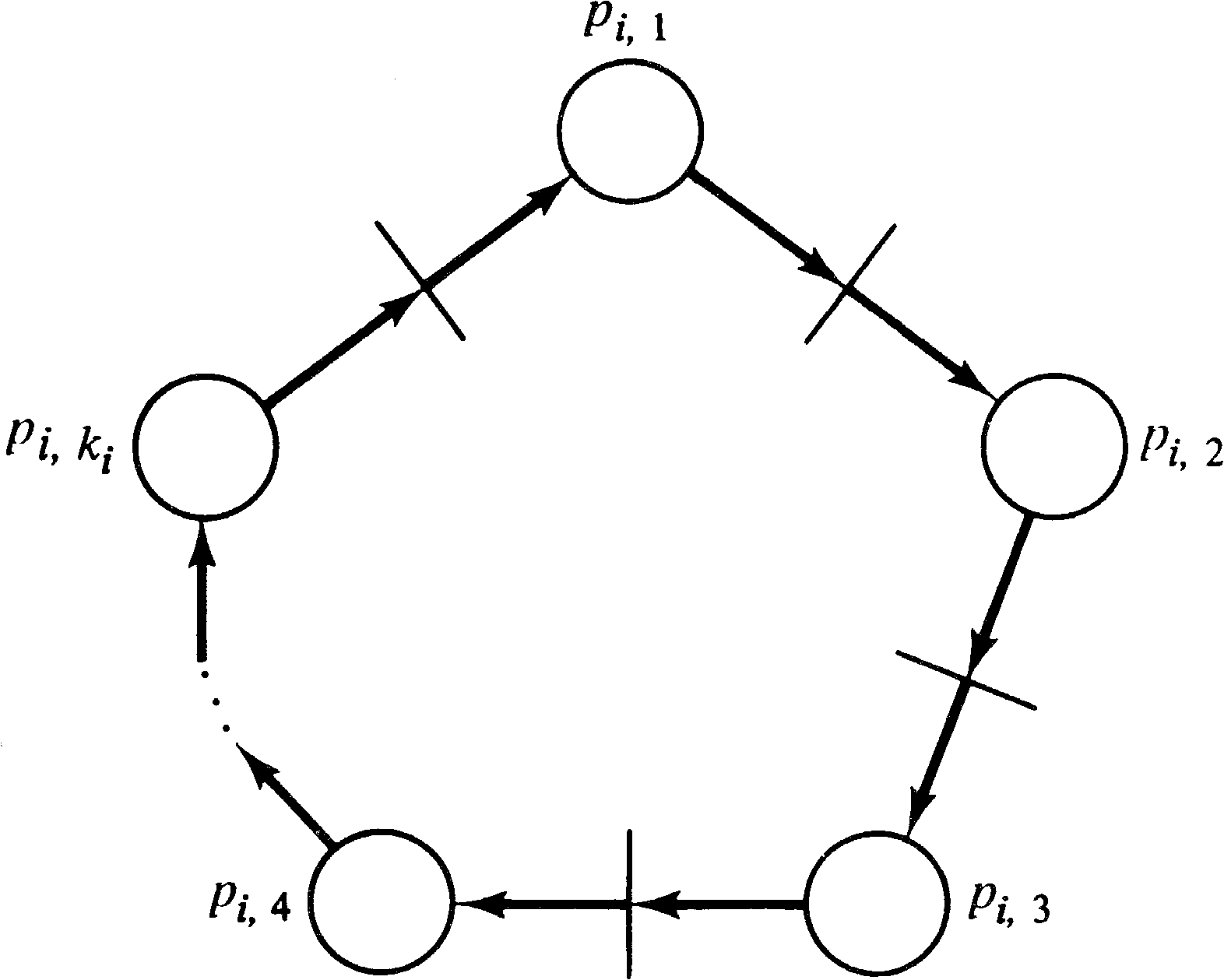
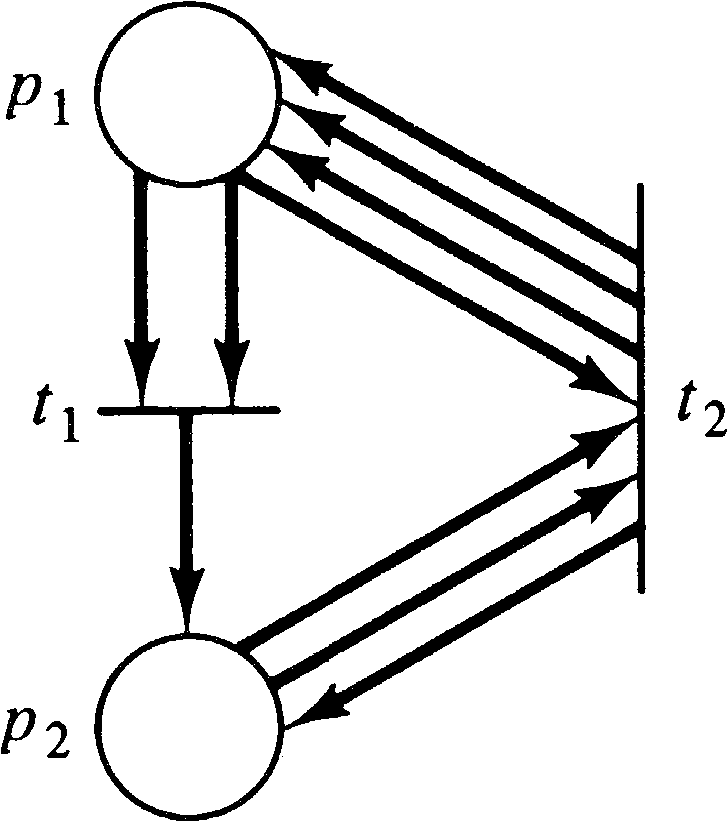
To transform a general Petri net into a restricted Petri
net, we use the following basic approach. Every place in
the general Petri net is replaced by a ring of places
in the restricted Petri net. Figure 5.4 shows the general
form of a ring of places. Notice that a collection of
tokens placed in the ring can freely move around the ring to
any position at any time; they can all group into place
pi,1 or spread out uniformly to cover all
ki places in the ring. Thus a transition
which needs three tokens from place pi can
pick up one from each of pi,1, pi,2,
and pi,3 rather than
all three from pi. Similarly a transition
which uses pi both as an input and as an
output (a self-loop) may input from pi,1 and
output to pi,2, eliminating the self-loop.
Formally, for a general Petri net
C1 = (P1, T1, I1, O1 )
with marking μ1, we define a
restricted Petri net
C2 = (P2, T2, I2, O2 )
with marking μ2 as follows. First define, for
each pi ∈ P1, an integer
ki by
| ki | = | max | (#(pi, I(tj)) + #(pi, O(tj))) |
| tj ∈ T1 |
| P2 | = | { p i, h | pi ∈ P1, 1 ≤ h ≤ ki } |
| T2 | = | T1 ∪ { t i, h | p i, h ∈ P2 } |
| #(p i, h , I2(tj)) | = | 1 if 1 ≤ h ≤ #(pi, I1(tj)) |
| = | 0 otherwise | |
| #(p i, h , O2(tj)) | = | 1 if #(pi, I1(tj)) < h ≤ #(pi, I1(tj)) + #(pi, O1(tj)) |
| = | 0 otherwise |
| I2(t i, h ) | = | { p i, h } | ||
| O2(t i, h ) | = | { p i, n | n | = | 1 + (h mod ki) } |
| μ2(pi,1) | = | μ1(pi) for pi ∈ P1 |
| μ2(p i, h ) | = | 0 for h > 1 |
By construction, for any marking μ which is reachable in
C1, there exists a marking μ′ of C2 such
that
| Σ | μ′(p i, h ) | = | μ(pi) for all pi ∈ P1 |
| h |
| μ′(pi,1) | = | μ(pi) for pi ∈ P1 |
| μ′(p i, h ) | = | 0 for h > 1 |
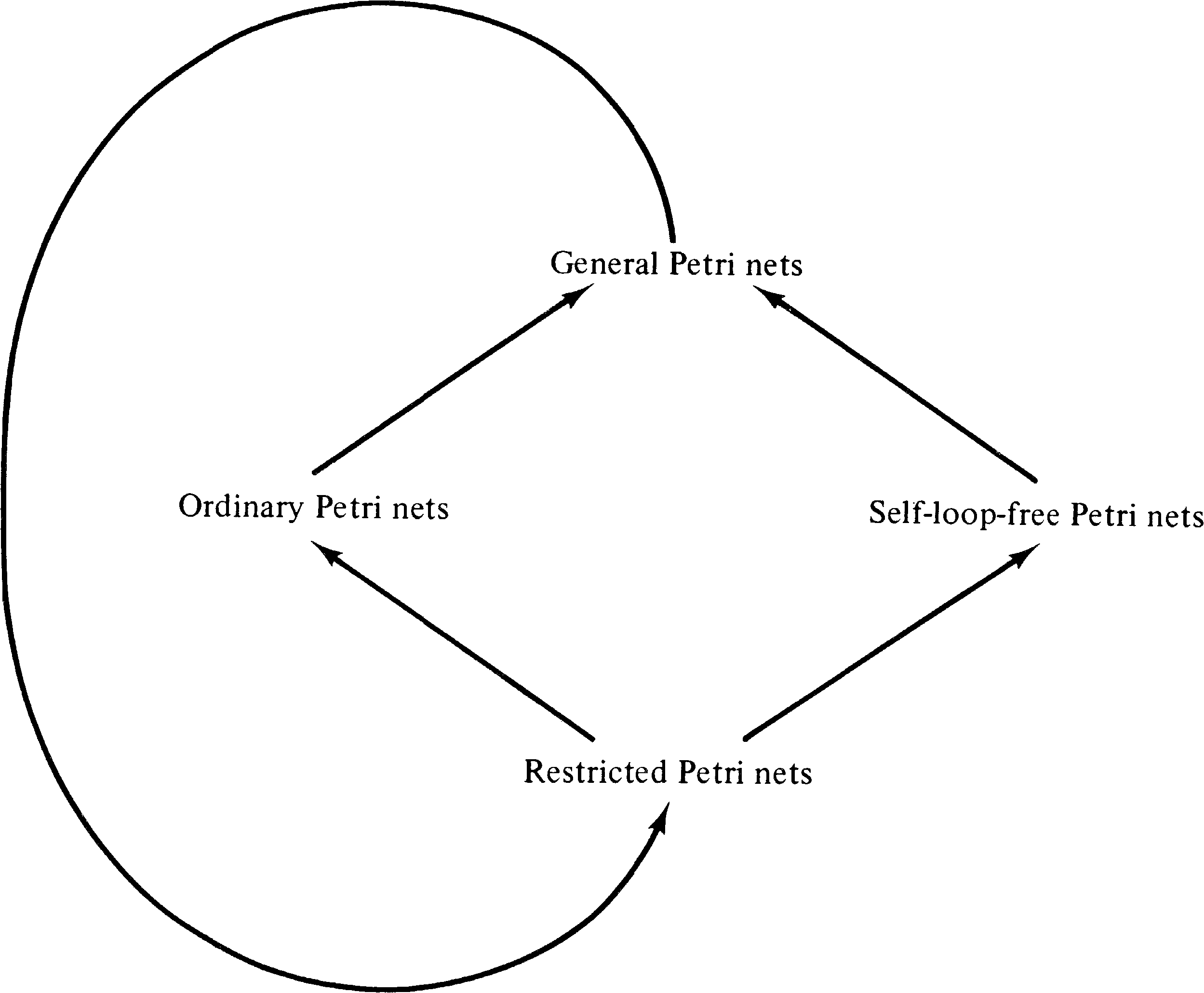
Thus, from the point of view of analysis, general Petri nets and these three
restricted classes of the general Petri net -- ordinary Petri
nets, self-loop-free Petri nets, and restricted Petri nets --
are equivalent, each can be transformed into a similar net
of another class, allowing a reachability problem in one to
be reduced to a reachability problem in another. The
constructions in this section are due to Hack [1974a].
Reachability is an important problem, but not the only remaining problem for Petri nets. Liveness is another problem which has received much attention in the Petri net literature. As pointed out in Section 4.1.4, liveness is related to deadlock. Two liveness problems for a Petri net C = (P, T, I, O) with initial marking μ are of concern here. A Petri net is live if each transition is live. A transition tj is live in a marking μ if for each μ′ ∈ R ( C, μ ) there exists a sequence σ such that tj is enabled in δ ( μ′, σ ) . A transition tj is dead in a marking μ if there is no reachable marking in which it can fire.
The liveness problem is obviously reducible to the single-transition liveness problem. To solve the liveness problem, we simply solve the single-transition liveness problem for each tj ∈ T; if | T | = m, then we must solve m single-transition liveness problems.
The reachability problem can also be reduced to the liveness problem. Since the many variants of the reachability problem are equivalent, we use the single-place zero-reachability problem. If we have any of the other reachability problems, they can be reduced to the single-place zero-reachability problem as shown in Section 5.2. Now, if we wish to determine if place pi can be zero in any reachable marking for a Petri net C1 = (P1, T1, I1, O1 ) with initial marking μ1, we construct a Petri net C2 = (P2, T2, I2, O2 ) with initial marking μ2, which is live if and only if the zero marking is not reachable from μ1.
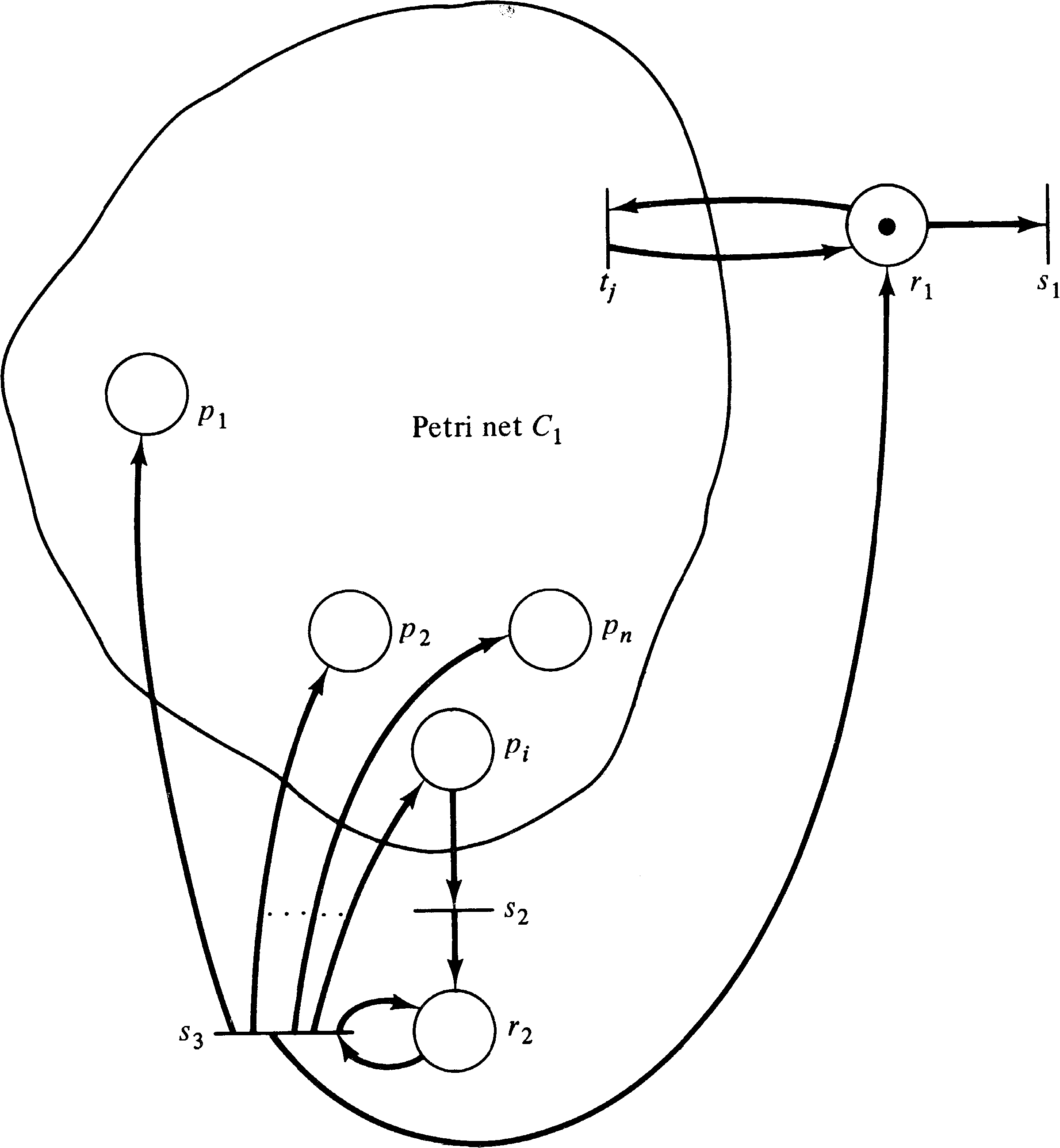
The Petri net C2 is constructed from C1 by the addition of two places, r1 and r2, and three transitions, s1, s2, and s3. We first modify all transitions of T1 to include r1 as both an input and an output. The initial marking μ2 will include a token in r1. The place r1 is a “run” place; as long as the token remains in r1 the transitions of T1 can fire normally. Thus any marking which is reachable in the places of P1 in C1 is also reachable in C2. Transition s1 is defined to have r1 as its input and a null output. This allows the token in r1 to be removed, disabling all transitions in T1 and “freezing” the marking of P1. (Note that all transitions of T1 are in conflict and, by construction if not by definition, that no more than one transition can fire at a time.)
The place r1 and transition s1 allow the
net C1 to reach any reachable marking and then for
s1 to fire and freeze the net at that marking. Now
we need to see if place pi is zero. We
introduce a new place r2 and a transition
s2 which has pi as its input and
r2 as its output. If pi can ever
become zero, this transition is not live; in fact the entire
net is dead if transition s1 fires in that
marking. Hence if pi can be zero, the net
is not live. If pi cannot be zero, then
s2 can always fire, putting a token in
r2. In this case we must put a token back in
r1 and assure that all transitions in C2 are
live. We must be sure that C2 is live even if C1 is
not live. This is accomplished by a transition s3
which “floods” the net C2 with tokens, assuring that
every transition is live if a token is ever put in
r2. Transition s3 has r2 as
its input and every place of C2 (all pi
in C1 and r1 and r2 ) as output.
This construction is illustrated in Figure 5.6.
Now, if a marking μ is reachable in R ( C1, μ1 ) with μ ( pi ) = 0, then the net C2 can also reach this marking on the place of P1 by executing the same sequence of transition firings. Then s1 can fire, freezing the C1 subset. Since μ ( pi ) = 0, transition s2 cannot fire and C2 is dead. Thus if pi can become zero, then C2 is not live.
Conversely, if C2 is not live then, a marking μ must be reachable in which μ ( r2 ) = 0 and there is no reachable state in which r2 has a token. [If r2 has a token, s3 is enabled, and s3 can be fired repeatedly enough times to enable any (or all) transitions, and so the net is live.] If r2 has no token and cannot get any, then the marking of pi must also be zero. Thus if C2 is not live, then a marking is reachable in which the marking of pi is zero.
On the basis of this construction, we have the following.
Now we need to show the following.
The proof that the single-transition liveness problem is reducible to the reachability problem rests on testing for the reachability of any of a finite set of maximal tj -dead submarkings. A Petri net is not live for a transition tj if and only if any marking is reachable in which the transition tj is not fireable and cannot become fireable. A marking of this sort is called tj -dead. For any marking μ we can test if it is tj -dead by constructing the reachability tree with μ as the root and testing if transition tj can fire anywhere in the tree. If it cannot then μ is tj -dead. Checking for liveness of tj then requires checking if any tj -dead marking is reachable.
In general, however, there may be an infinite number of tj -dead markings and an infinite set of markings in which to find the tj -dead markings. The set of markings which must be checked for reachability is reduced to a finite number by noting two properties. First, if a marking μ is tj -dead, then any marking μ′ ≤ μ is also tj -dead. (Any firing sequence possible from μ′ is also possible from μ, so if μ′ could lead to the firing of tj, so could μ .) Second, the markings of some places will not affect the tj -deadness of a marking, and so the markings of these places are “don't-cares”; they can be arbitrary. Borrowing from the reachability tree construction, we replace these “don't-care” components by ω to indicate that an arbitrarily large number of tokens can be in this place without affecting the tj -deadness of the marking. Now since any μ′ ≤ μ is tj -dead if μ is tj -dead, we need not consider those places pi with μ ( pi ) = ω . This means we use the submarking reachability problem with P′ = { pi | μ ( pi ) ≠ ω } .
As an example, consider the Petri net of Figure 5.7. The
markings (2, 0), (1, 0), (0, 0), (0, 1), (0, 2), (0, 3), …
are tj -dead, but they can be finitely
represented by the set { (0, ω ), (2, 0), (1, 0) } .
Hack [1974c; 1975c] has shown that there exists for a Petri net C a finite set Dt of markings (extended to include ω ) such that C is live if and only if no marking in Dt is reachable. If a marking of Dt contains ω, submarking reachability is implied.
Further, Dt can be effectively computed. Since Dt is finite, the non- ω -components of the markings have an upper bound b. This bound b is characterized as the smallest number such that for any marking μ with μ ( pi ) ≤ b + 1 for all pi, if μ is tj -dead, then the submarking μ′, with μ′ ( pi ) = μ ( pi ) if μ ( pi ) ≤ b and μ′ ( pi ) = ω if μ ( pi ) = b + 1, is tj -dead. With this characterization of b, we can construct Dt as follows.
From these two theorems, we have the following.
More formal proofs of the reducibility of liveness to
reachability can be found in [Hack 1974c; Hack 1975c].
5.5. Undecidable Results
In Section 5.4 we have shown that a number of problems in reachability and liveness are equivalent, but no result has been obtained yet on the decidability of these problems. To show decidability, it is necessary to reduce a Petri net problem to a problem with a known solution, or to show undecidability, to reduce a problem which is known to be undecidable to a Petri net problem. The first important result of this kind was by Rabin [Baker 1973b]. Rabin showed that for two Petri nets C1 with marking μ1 and C2 with marking μ2 it is undecidable if R ( C1, μ1 ) ⊆ R ( C2, μ2 ) . Hack [1975a] later strengthened this to show that it is undecidable if R ( C1, μ1 ) = R ( C2, μ2 ) . The proof of these statements is based on Hilbert's tenth problem. (In 1900, D. Hilbert presented 23 problems to a conference of mathematicians; this was the tenth in his list.)
| P(x1, x2, …, xn) | = | 0? |
The equation
P ( x1, x2, …, xn ) = 0
is a Diophantine equation.
In general it will be a sum of terms
| P(x1, x2, …, xn) | = | Σ | Ri(x1, x2, …, xn) |
| i | |||
| Ri(x1, x2, …, xn) | = | ai ⋅ x s1 ⋅ x s2 ⋅ ⋯ ⋅ x sh | |
In 1970, Matijasevic proved that Hilbert's tenth problem was
undecidable [Davis 1973; Davis and Hersh 1973]: There is no
general algorithm to determine if an arbitrary Diophantine
equation has a root (a set of values for which the
polynomial is zero). This forms the basis of the proof that
the equality problem for Petri net reachability sets is
undecidable. The strategy is to construct for a Diophantine
polynomial a Petri net which (in some sense) computes all
values of the polynomial.
5.5.1. The Polynomial Graph Inclusion Problem
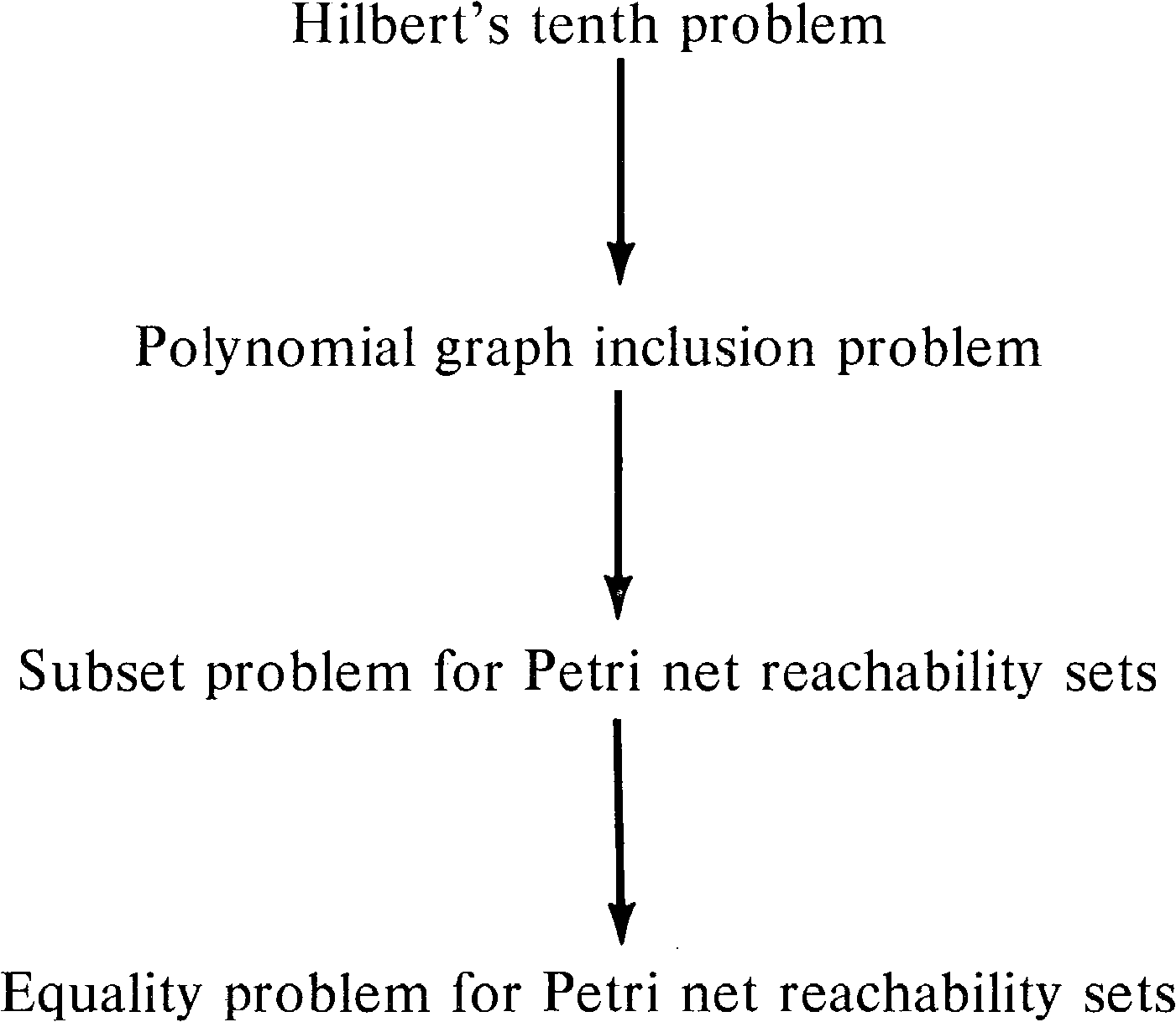
The proof of the undecidability of the equality problem is
in three parts (Figure 5.8). First, Hilbert's tenth problem is reduced
to the polynomial graph inclusion problem. Then the
polynomial graph inclusion problem is reduced to the
subset problem for Petri net reachability sets.
Finally, the subset problem for Petri net reachability sets
is reduced to the equality problem for Petri net
reachability sets. This shows that Hilbert's tenth
problem, known to be undecidable, is reducible to the
equality problem, which must therefore also be undecidable.
| G(P) | = | { (x1, …, xn, y) | y ≤ P(x1, …, xn) with 0 ≤ x1, …, xn, y } |
| G(Q1) | = | { (x1, …, xn, y) | y ≤ Q1(x1, …, xn) } |
| G(Q2 + 1) | = | { (x1, …, xn, y) | y ≤ 1 + Q2(x1, …, xn) } |
| Q1(x1, …, xn) < y ≤ 1 + Q2(x1, …, xn) |
| Q1(x1, …, xn) < y ≤ 1 + Q2(x1, …, xn) ≤ 1 + Q1(x1, …, xn) |
| y | = | 1 + Q2(x1, …, xn) | = | 1 + Q1(x1, …, xn) |
Now we need to show that Petri nets can (in some sense)
compute the value of a polynomial
Q ( x1, x2, …, xn ) .
We have carefully
limited the polynomial Q to having a nonnegative value,
nonnegative coefficients, and nonnegative variables. This
allows us to encode the values of the variables and the
value of the polynomial as the number of tokens in places in
a Petri net. Figure 5.9 shows the general scheme. The
input values x1, …, xn
are encoded by xi tokens
in pi for i = 1, …, n.
Initially a token also resides in the “run” place. The
execution of the net will terminate by placing a token in
the “quit” place. At this time the “output” place will have
y tokens,
where y ≤ Q ( x1, …, xn ) .
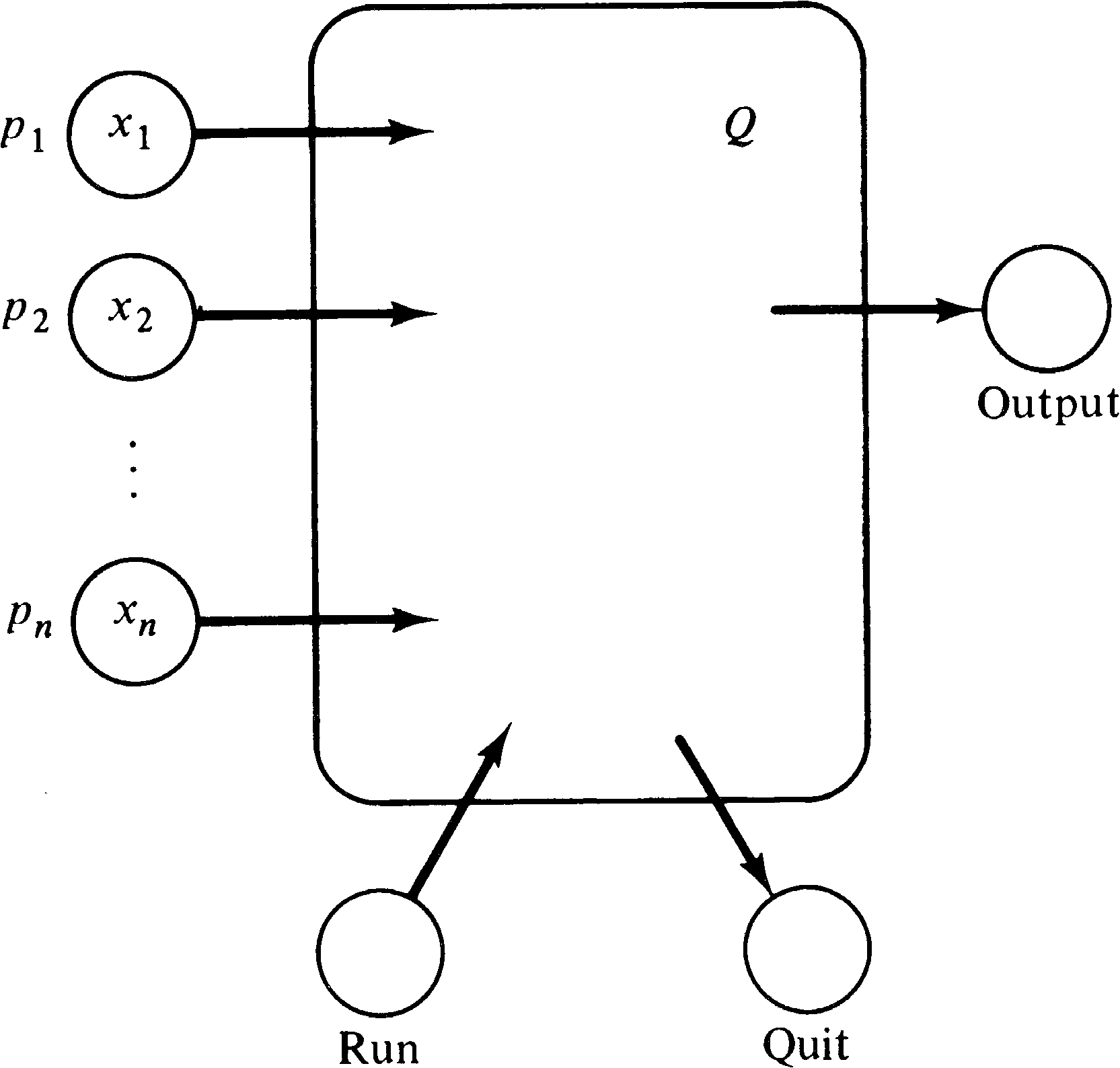
This Petri net will weakly compute the value Q ( x1, …, xn ) . Weak computation means that the value computed will not exceed Q ( x1, …, xn ) but may be any (nonnegative) value less than Q ( x1, …, xn ) . Weak computation is necessary for Petri nets because of the permissive nature of transition firings; a Petri net cannot be forced to finish. The definition of a polynomial graph G ( Q ) was made specifically with this in mind.
What we show now is that subnets can be constructed which weakly compute the function of (binary) multiplication. From this, we can construct a composite net which weakly computes the value of each term of a polynomial by successive multiplication subnets. The output of the subnet for each term will be deposited in the output place for the polynomial. Thus the number of tokens in the output place will be the sum of the outputs for each term.
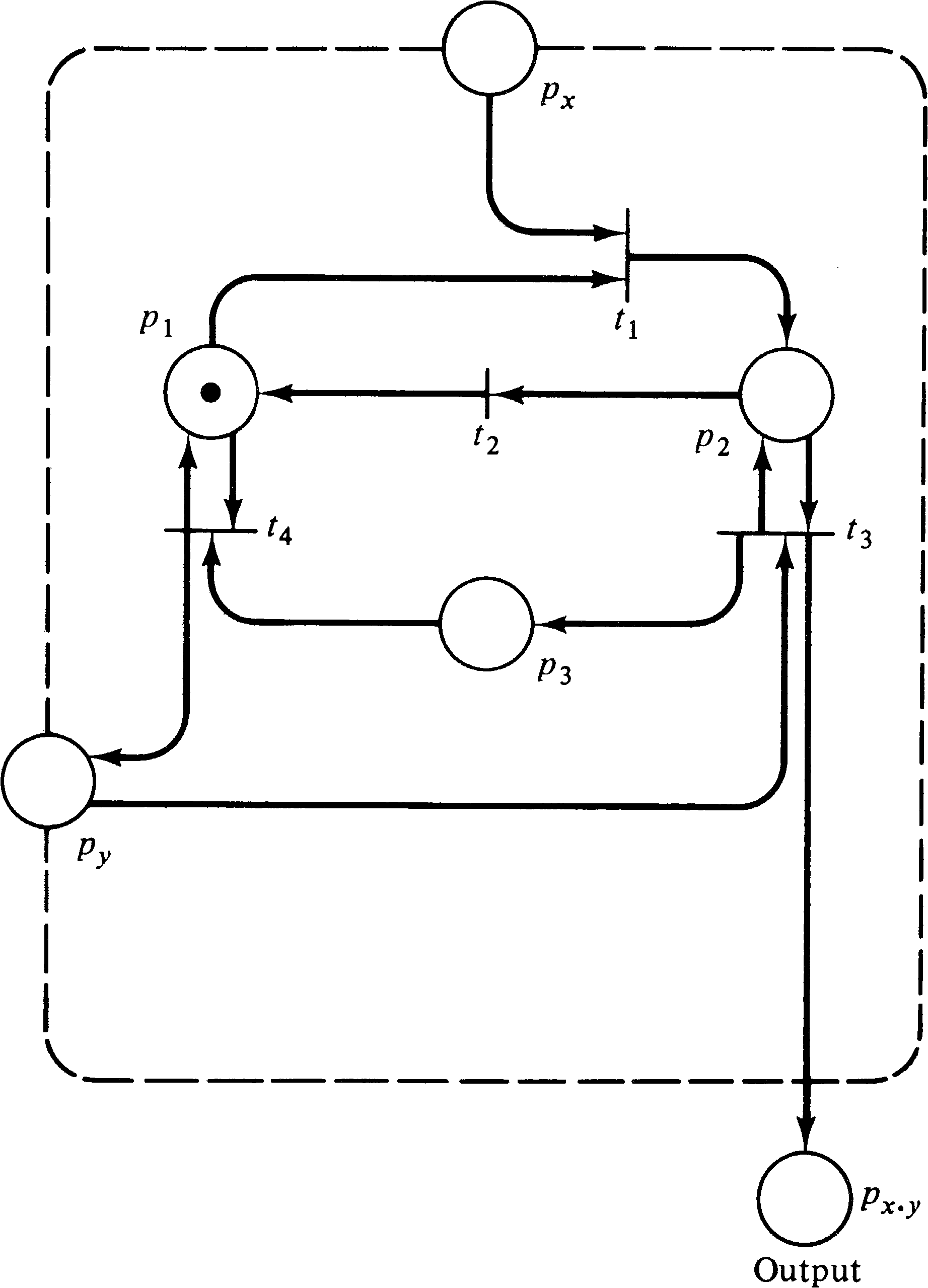
The multiplication subnet is shown in Figure 5.10. This net
will weakly compute the product of the numbers, x and
y, of tokens in its two inputs and place this many
tokens in its output. The operation of the net is quite
simple. To compute the product of x and y,
transition t1 first fires, moving one token from
px to p2. This token enables
transition t3, which can now copy y tokens
from place py, putting them in p3
and putting y tokens in
p x ⋅ y ,
the output place. Now t2 can fire,
putting the token in p2 back into p1.
This enables t4, which can copy the y tokens
from p3 back into py. This entire
process can be repeated exactly x times, each time
putting y tokens in p x ⋅ y .
Then the marking of place px has
been reduced to zero, and the net must stop. The total
number of tokens in place p x ⋅ y
is then the product of x and y.
The above case is the best case, in the sense that the
number of output tokens is exactly x ⋅ y.
However, the token in p2 enables both transitions
t3 and t2, and it is possible for
t2 to fire before all y tokens have been
copied from py to p3 and been
added to p x ⋅ y . In this case,
the number of tokens deposited in
p x ⋅ y
will be less than x ⋅ y. Since
t3 can fire no more than y times for each
firing of t1 and t1 can fire no more
than x times, we can guarantee that the number of
tokens in p x ⋅ y never exceeds
x ⋅ y, but because of the permissive
nature of transition firings, we cannot guarantee that the
number of tokens in p x ⋅ y will
actually equal x ⋅ y; it could be less.
Thus, this Petri net weakly computes the product of x
and y. Now to weakly compute a term Ri which
is the product ai x s1 x s2... x sh
we construct a Petri
net of the form shown in Figure 5.11. Since each subnet
weakly computes the product of two terms, the entire subnet
weakly computes the value of the term Ri.
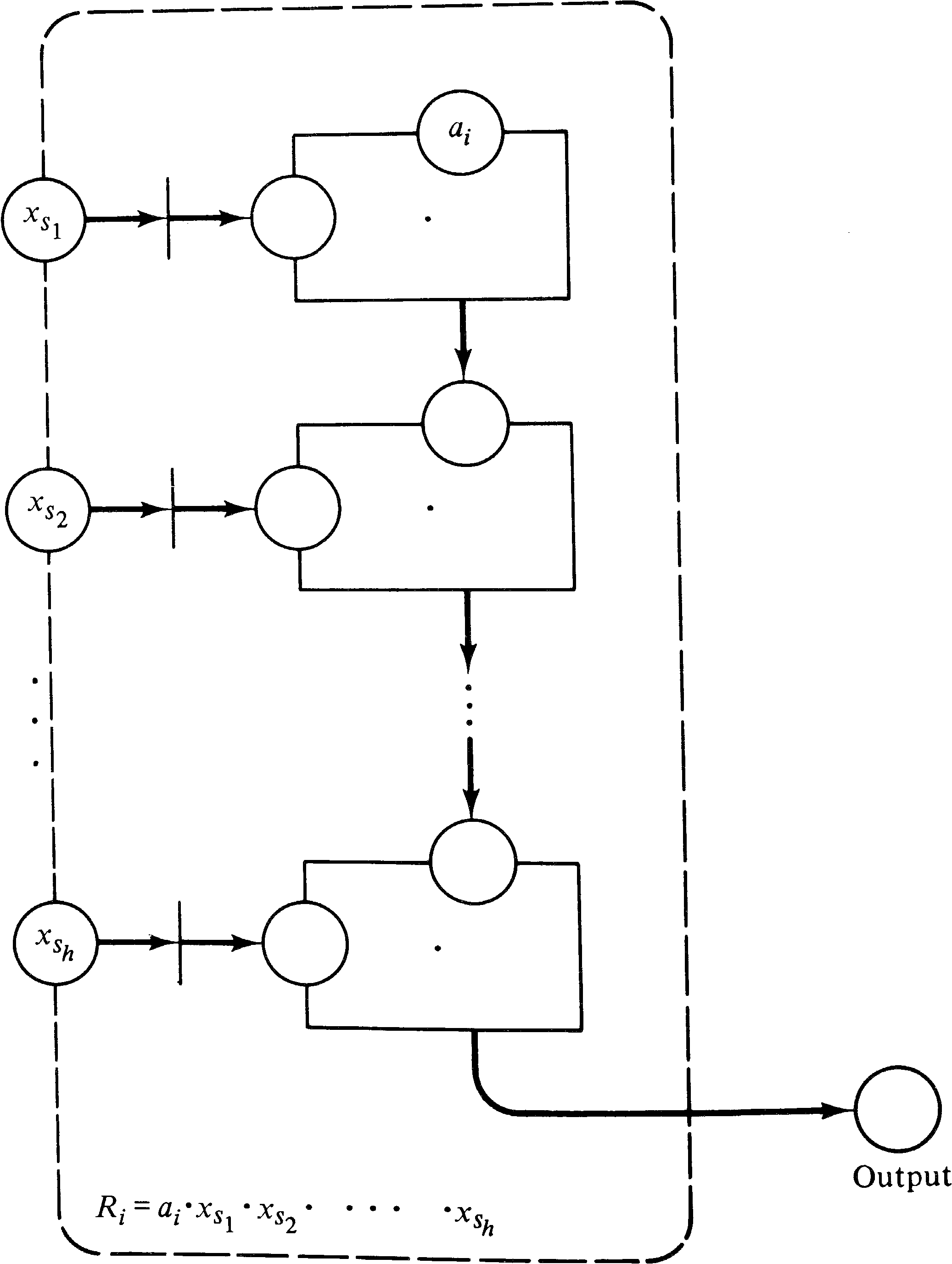
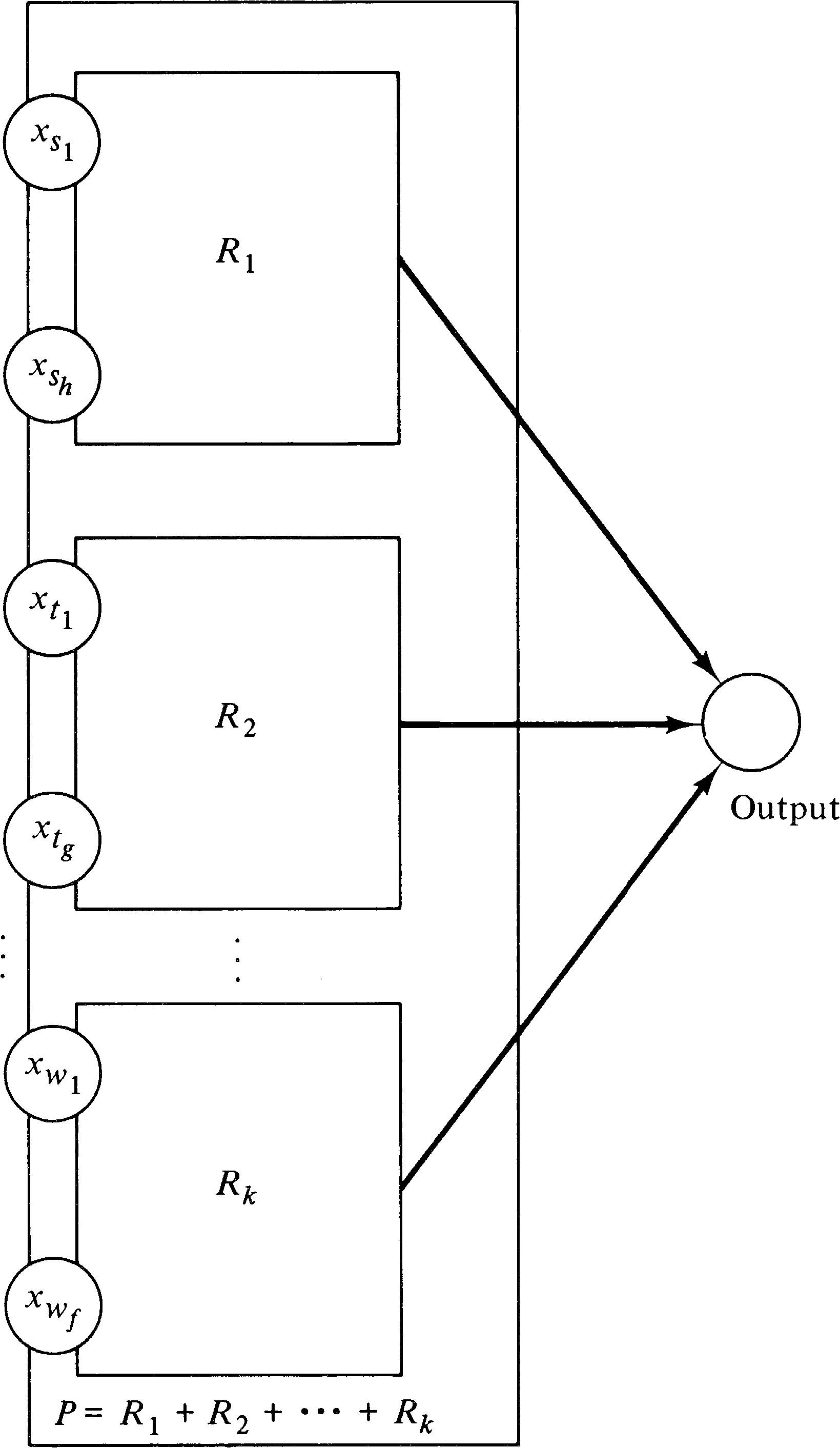
Figure 5.12 then shows how a polynomial
P = R1 + R2 + ⋯ + Rk
can be weakly computed. Each subnet is
of the form of Figure 5.11 and weakly computes the value of
one term. The outputs of the k subnets for each term
have been merged together, giving a total value which is the
sum of each term.
Now some control transitions and places are added to create the specific reachability sets needed. First we need to be able to produce an arbitrary value for each of the variables ( x1, …, xn ) and record that value in the places p1, …, pn. A transition ti is created for each pi with null input and outputs to pi and every place which is an input corresponding to xi in a term Rj which uses xi. Thus, in the polynomial x1 + x1 x2 we would have a transition t1 with outputs to p1 and to the x1 inputs of the two terms, x1 and x1 x2, which use x1; t2 would output to p2 and to the x2 input of the term x1 x2.
These transitions can fire an arbitrary number of times, creating any value in p1, …, pn. Thus, for every y ≤ P ( x1, …, xn ) a marking μ is reachable with μ ( p1 ) = x1, …, μ ( pn ) = xn and μ ( output ) = y. The value y = P ( x1, …, xn ) can be achieved by first firing t1 x1 times, putting x1 tokens in p1, then firing t2 x2 times, and so on until tn has fired xn times. The subnet for each term Ri of the polynomial can then execute, with the resulting polynomial value put in the output place.
To reduce the polynomial graph inclusion problem to the subset problem for Petri net reachability sets, we perform the following steps. For polynomials A and B, we wish to determine if G ( A ) ⊆ G ( B ) .
To prevent this problem we add two new places q and r to CA (giving CA′ ) and q′ and r′ to CB (giving CB′ ). In CA′, q, and r are not used for any transitions, and initially r is empty and q is marked with one token. In CB′, r′ is a “run” place. It is initially marked, and every transition in CB′ is modified to include r′ as both an input and an output. Thus, as long as the token remains in r′, the net CB′ can function as before. A new transition transfers the enabling token from r′ to q′, disabling all transitions in CB′ and “freezing” the marking. Now we add two new transitions for each internal place in CB′ .
For each internal place pi whose marking is unimportant, one transition has places q′ and pi as inputs and only q′ as an output (allowing the marking in pi to be decreased by one), and another transition has q′ as input and both q′ and pi as outputs (allowing the marking in pi to be increased by one). These transitions allow the marking of each internal place to be made arbitrary by an appropriate sequence of increasing or decreasing firings.
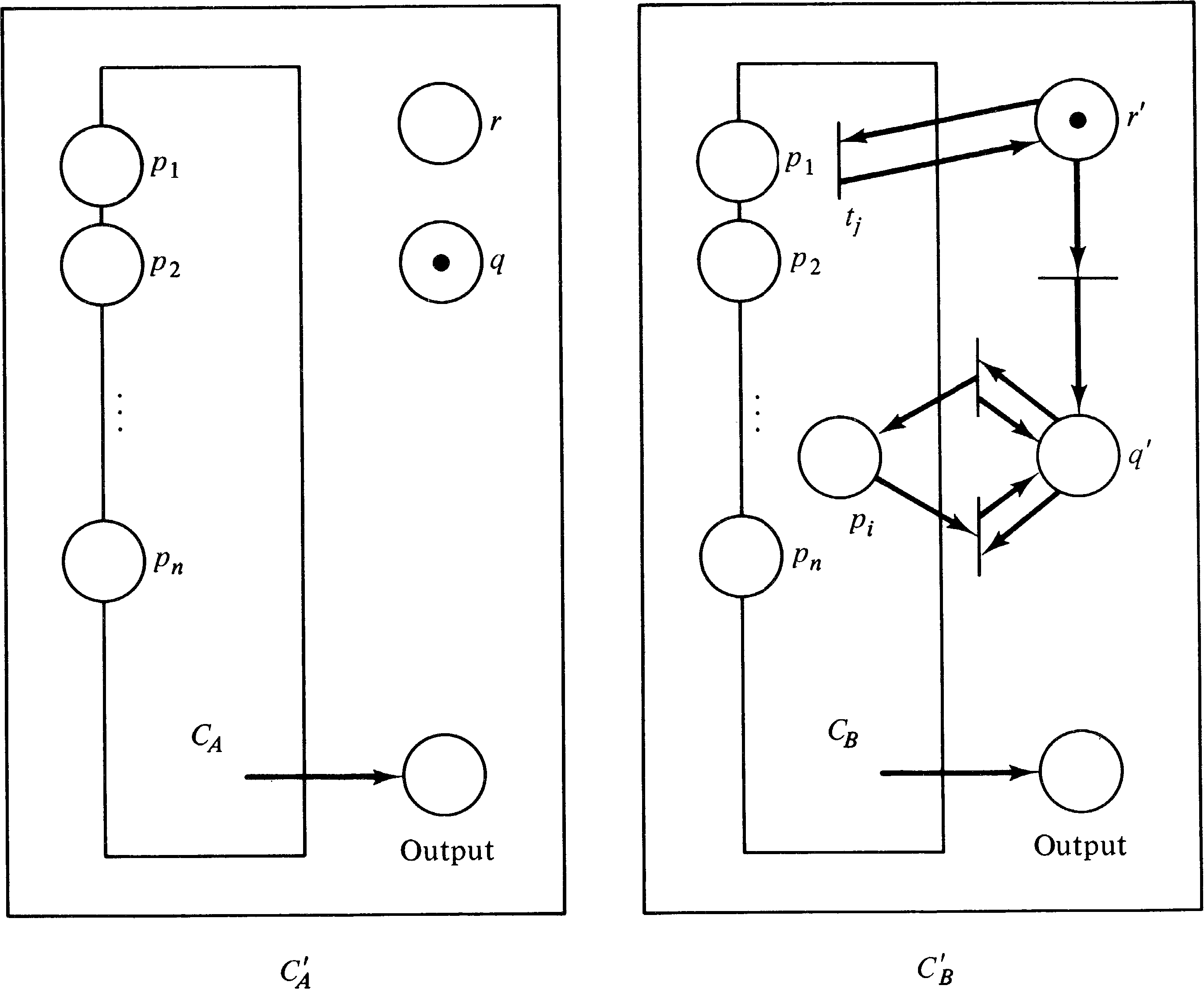
The reachability sets of CA′ and CB′ are
as follows.
For CA′,
| p1 | ... | pn | output | r | q | internal places |
| x1 | ... | xn | y ≤ A(x1, …, xn) | 0 | 1 | Some arbitrary marking |
| p1 | ... | pn | output | r | q | internal places |
| x1 | ⋯ | xn | y ≤ B(x1, …, xn) | 1 | 0 | Some arbitrary marking |
| x1 | ⋯ | xn | y ≤ B(x1, …, xn) | 0 | 1 | All arbitrary markings |
This concludes our demonstration of the following.
We now have only to show that the subset problem for Petri net reachability sets is reducible to the equality problem.
Assume that we have two Petri nets A and B and wish to
determine if R ( A, μA ) ⊆ R ( B, μB )
(the subset problem). We now show
that two Petri nets D and E can be defined
such that R ( A, μA ) ⊆ R ( B, μB )
if and only if
R ( D, μD ) = R ( E, μE ) . The basis for this
construction is the fact that
| R(A, μA) ⊆ R(B, μB) if and only if R(B, μB) | = | R(A, μA) ∪ R(B, μB) |
Both D and E are constructed from a common subnet, C. The
net C encodes the reachability sets of both A and B in such
a way as to produce their union. Figure 5.14 illustrates
the basic construction. The n places
p1, …, pn act as either the
n places of net A or the n places of net B.
Originally they are unmarked. Two new places rA
and rB are added as “run” places for net A and net
B, respectively. All transitions of net A are modified to
include rA as both an input and an output; all
transitions of net B are modified to include rB as
both an input and an output.
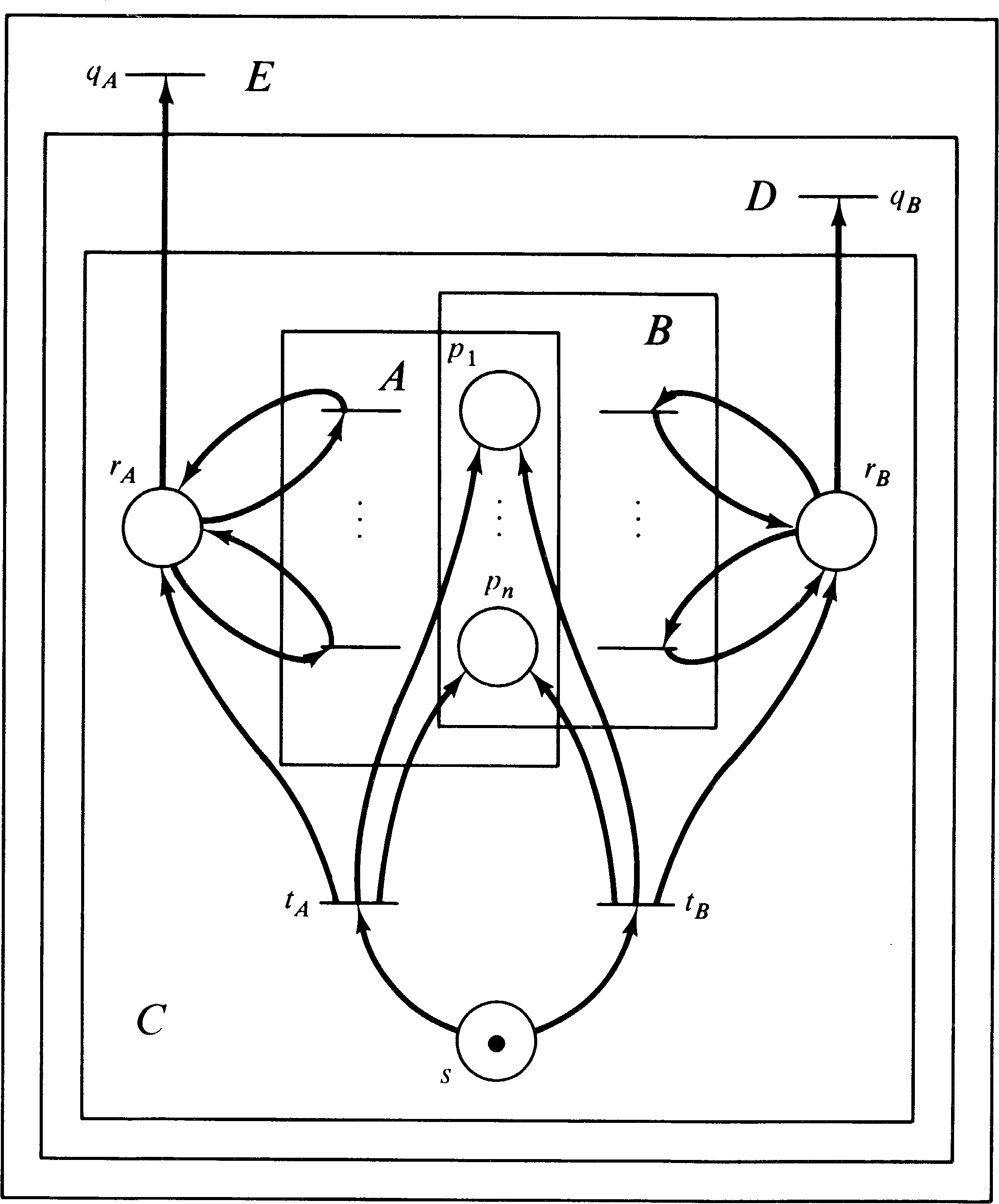
Now, one more place, s, is added and two new
transitions, tA and tB. The initial
marking for this entire net (including A and B as subnets
with shared places; places rA, rB, and
s; and transitions tA and tB ) is
one token in s and zero tokens elsewhere. Transition
tA has place s as its input and as output
produces the initial marking for net A plus a token in
rA; transition tB has place s as
its input and produces the initial marking for net B plus a
token in rB. Thus, if tA fires, then
the subnet A has its initial marking, and all of its
transitions can fire as normal since there is a token in
rA. However, subnet B is completely disabled,
since there is no token in rB. If tB
fires first, then the subnet B can operate, and A is
disabled. The set of firing sequences for C is then any
sequence of the form
| tA, < any sequence of firings from A> |
| tB, < any sequence of firings from B> |
The net D is obtained from C by adding one new transition, qB. Transition qB has place rB as its input and no output. Notice that qB can fire only if transition tB was the first to fire; if transition tA fires first, then rB will be empty, and tB cannot fire.
The net E is constructed from D by adding a new transition, qA. Transition qA has place rA as its input and no output. Transition qA can fire only if tA was the first to fire: Notice that net E is constructed from D, not (directly) from C. So E has both transition qA and transition qB.
Now let us examine the reachability sets of the Petri nets
C, D, and E. The reachability set of C is all markings of
the form
| s | rA | rB | p1, …, pn |
| 1 | 0 | 0 | 0, …, 0(initial marking) |
| 0 | 1 | 0 | Any μ ∈ R(A, μA) (if tA fires) |
| 0 | 0 | 1 | Any μ ∈ R(B, μB) (if tB fires) |
| s | rA | rB | p1, …, pn |
| 1 | 0 | 0 | 0, …, 0(initial marking) |
| 0 | 1 | 0 | Any μ ∈ R(A, μA) (if tA fires) |
| 0 | 0 | 1 | Any μ ∈ R(B, μB) (if tB fires) |
| 0 | 0 | 0 | Any μ ∈ R(B, μB) (if qB fires) |
| s | rA | rB | p1, …, pn |
| 1 | 0 | 0 | 0, …, 0(initial marking) |
| 0 | 1 | 0 | Any μ ∈ R(A, μA) (if tA fires) |
| 0 | 0 | 1 | Any μ ∈ R(B, μB) (if tB fires) |
| 0 | 0 | 0 | Any μ ∈ R(B, μB) (if qB fires) |
| 0 | 0 | 0 | Any μ ∈ R(A, μA) (if qA fires) |
Now, if R ( A, μA ) ⊆ R ( B, μB ), the
last class in R ( E, μE ) [markings of the form (0, 0, 0, μ ) with μ ∈ R ( A, μA ) ] is included in
the last class of R ( D, μD ) [markings of the form
(0, 0, 0, μ ) with μ ∈ R ( B, μB ) ]. Since all
other markings are the same,
| R(D, μD) | = | R(E, μE) if R(A, μA) ⊆ R(B, μB) |
Thus, this construction shows the following.
The undecidability of the subset and equality problems for Petri net reachability sets creates the possibility that the reachability problem itself is also undecidable. However, at the moment, the decidability (or undecidability) of the reachability problem is open. There is currently neither an algorithm to solve the reachability problem nor a proof that such an algorithm cannot exist.
In 1977, a “proof” of the decidability of the reachability problem was presented at the ACM Symposium on Theory of Computing [Sacerdote and Tenney 1977]. However, this “proof” has several serious flaws, and attempts to correct them, to produce a correct proof, have been unsuccessful. Still the prevailing feeling is that the reachability problem is decidable -- it is believed that an algorithm does exists and will be discovered in time.
Assuming that an algorithm to solve the reachability problem does exist, it is likely to be very complex. The obvious question is, If an algorithm to solve the reachability problem exists, how complex must it be? Some bounds on this complexity can be established without reference to any specific algorithm
Lipton [1976] has shown that any algorithm to solve the reachability problem will require at least an exponential ( 2 c ⋅ n ) amount of space for storage and an exponential amount of time. The exponent ( n ) is a measure of the size of the problem and in Lipton's case reflects the number of places and their interconnections to transitions.
Lipton proved that exponential space is necessary by showing that a Petri net can be constructed in which a place acts as a counter of the numbers 0, 1, …, 22n. Representing this in the reachability problem algorithm would require at least log2 (22n ) = 2n bits. Just as important is that his construction uses at most h ⋅ n places (for some constant h ).
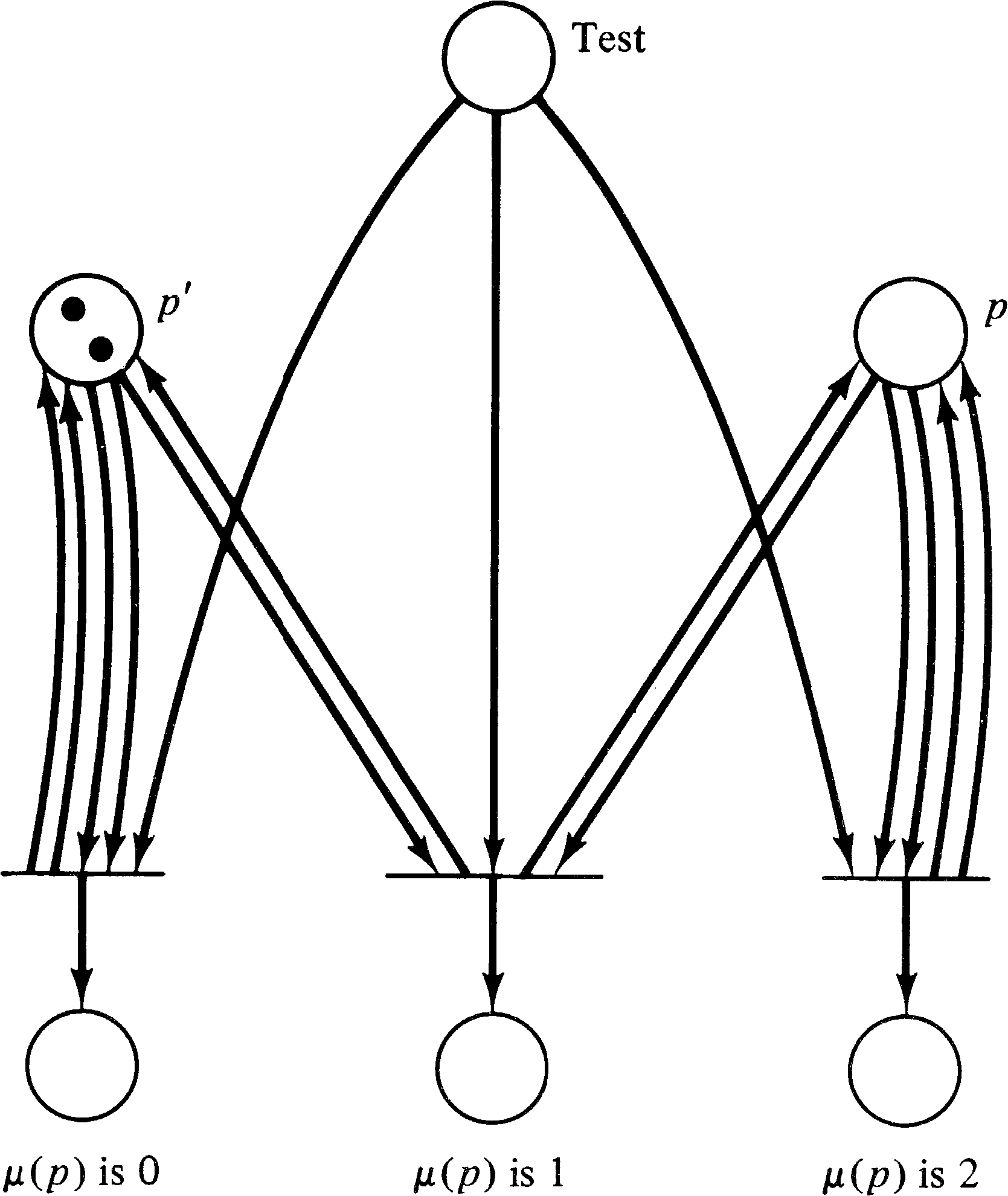
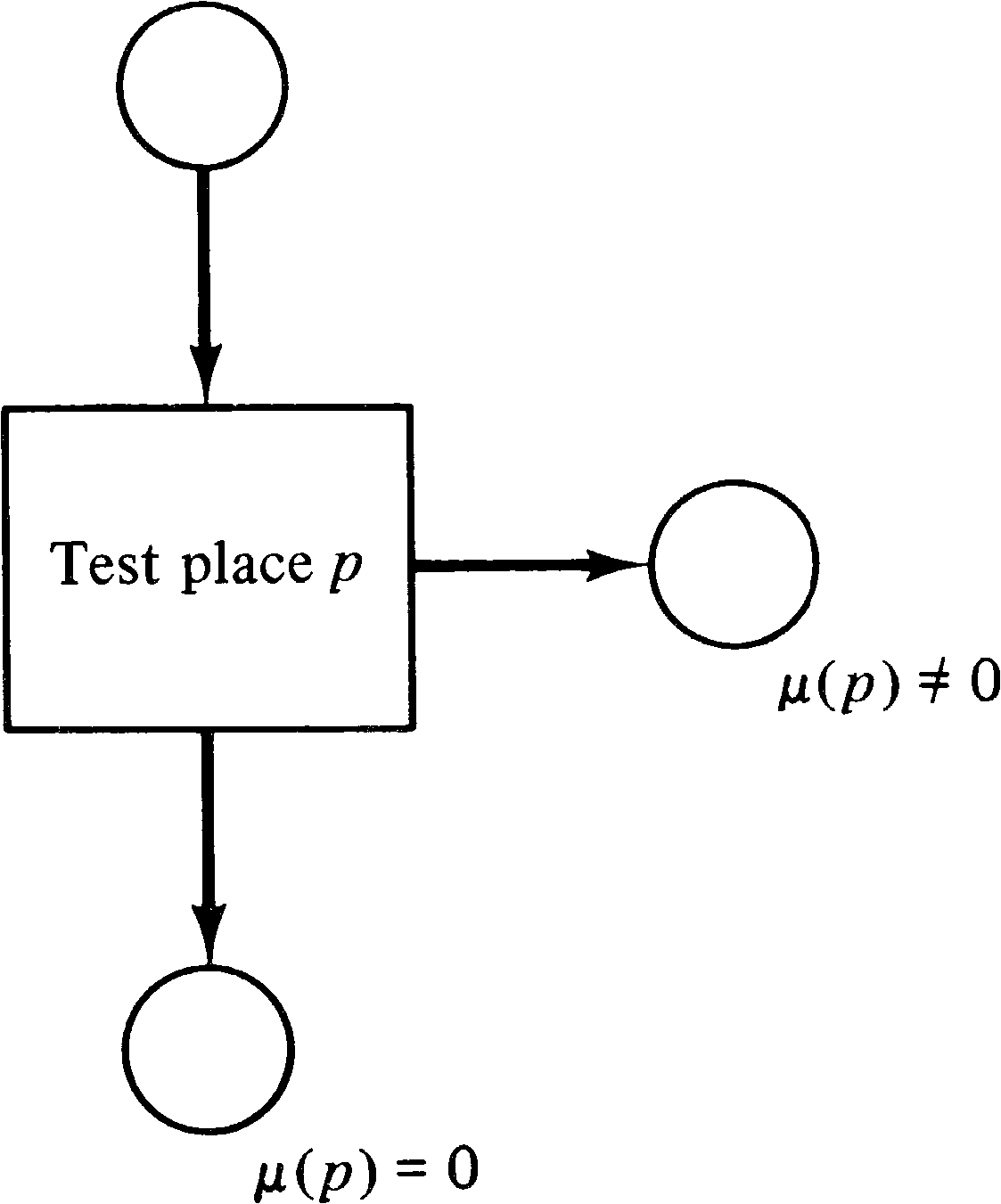
Lipton's proof hinges on the ability to create a net to count to 22n in only h ⋅ n places. Part of the constraints is a need to test this place for zero. Petri nets, of course, have been designed so that there is no direct way to test for zero. However, a common technique used with Petri nets to allow zero testing is to use two places p and p′ such that μ ( p ) + μ ( p′ ) is a constant. If we know that μ ( p ) + μ ( p′ ) = k, then we can test for μ ( p ) being zero by testing if μ ( p′ ) has k tokens; if μ ( p′ ) has k tokens, then μ ( p ) has zero tokens and vice versa. A place can be tested for nonzero by using it in a self-loop. Note that to maintain this ability we must maintain the constant nature of μ ( p ) + μ ( p′ ) ; that is, the net must be conservative, at least with respect to these two places.
For small numbers k one can test if the marking of a
place is k by having the place be an input to a
transition k times (Figure 5.15). However, these arcs contribute to
the size of the problem, and so we cannot do this in
general. Lipton showed that if the constant sum of two
places ( pk, pk′ ) is
k and k is a product of two smaller integer
factors k = k1 ⋅ k2 which
are the constant sums of two other pairs of places
( p k1, p k1′ and
p k2, p k2′ ) and
we can test μ ( p k1 ) = 0 and
μ ( p k2 ) = 0, then we can test if
μ ( pk ) = 0 . This allowed Lipton to build
subnets such as Figure 5.16. These nets are then used to
control multiplication nets, similar to the nets used to
weakly compute the polynomial graph (see Figure 5.10). The
test-for-zero subnet allows the Petri net to compute the
exact product (not a weak product which is merely bounded by
the real product).
These simple nets allow Lipton to build a net, for a given n, which can generate exactly 22n tokens in a place ( p ) with zero tokens in p′ and the ability to test μ ( p ) for zero. The number of places used is only a constant factor times n. The existence of a Petri net like this shows that the reachability problem requires exponential time and space and hence will be very expensive to solve.
The construction of a Petri net which can count up to 22n has a very important corollary, too. The Petri net which is constructed is bounded, since the number of tokens in any given place cannot exceed 22n. This means that any algorithm to determine boundedness of a Petri net must also require exponential time and space. Thus, even simple problems for Petri nets, while decidable, may require large amounts of time and space for solution.
It should be remembered that these are lower bounds on the worst-case behavior of an algorithm. It may be the case that many interesting problems can be decided for most Petri nets relatively efficiently. These complexity results show that even if an algorithm works very well most of the time there exists a Petri net which will take lots of time and space to analyze.
Although these are worst-case complexity results (which means the average case may be much better), they are also lower-bound results. We know that the reachability problem requires exponential space, at least. It may be that reachability is even worse than exponential. Rackoff [1976] has developed an algorithm for determining boundedness in exponential time, so the boundedness problem is known to be of exponential complexity. However, the reachability problem is simply known to be at least exponentially complex (and may not even be decidable).
A recent result by Mayr [1977] showed that the subset and
equality problems for bounded Petri net reachability
sets are of nonprimitive recursive complexity. These
results indicate that some problems for Petri nets, while
decidable, are computationally intractable.
Exercises
| P2 | = | P1 ∪ { pj′ | tj ∈ T1 } |
| T2 | = | T1 |
| I2 | = | I1 |
| O2(tj) | = | O1(tj) ∪ { pj′ } |
Computability theory is an early part of the theory of computation and developed from the work of Turing, Kleene, Godel, and Church. Davis [1958] and Minsky [1967] offer good explanations of this work. Karp [1972] shows how reducibility can be used for decidability and complexity results.
The reachability problem first arose in [Karp and Miller 1968]; it was reported as a research question in [Nash 1973]. Preliminary results were reported in [Van Leeuwen 1974; Hopcroft and Pansiot 1976], but these do not generalize.
Most of the results in this chapter are due to the work of
Hack [1974a; 1974c; 1975a; 1975c]. Hack has been one of the
major researchers on decision problems for Petri nets.
Other work on decision properties includes [Araki and Kasami 1976;
Araki and Kasami 1977; Mayr 1977].
Complexity results have been produced by Lipton [1976],
Rackoff [1976], and Jones et al. [1976] among
others. Some related work not directly tied to Petri nets
is [Cardoza 1975; Cardoza et al. 1976].
5.8. Topics for Further Study
| #(pi, I(tj)) | = | #(pi, O(tk)) |
| #(pi, O(tj)) | = | #(pi, I(tk)) |
| Home | Comments? |